Пошаговое объяснение:
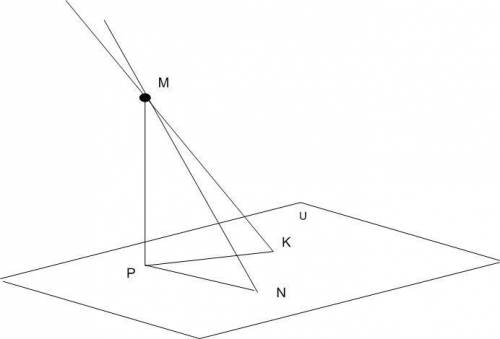
Задача 1. Файл "плоскость"
Дано:
плоскость u;
∠PMK =60°;
l PK l= 8√3;
l MN l=8√2.
Найти:
∠PMN
l PK l / l MP l = tg(∠PMK);
l MP l=l PK l/ tg(∠PMK);
l MP l=8√3/tg60°; tg60°=sin60°/cos60°=(√3/2)/(1/2)=√3;
l MP l=8√3/√3=8;
cos(∠PMN)=l MP l/l MN l;
cos(∠PMN)=8/(8√2)=1/√2=√2/(√2*√2)=√2/2;
∠PMN = arccos(√2/2)=45°
ответ:∠PMN = 45°
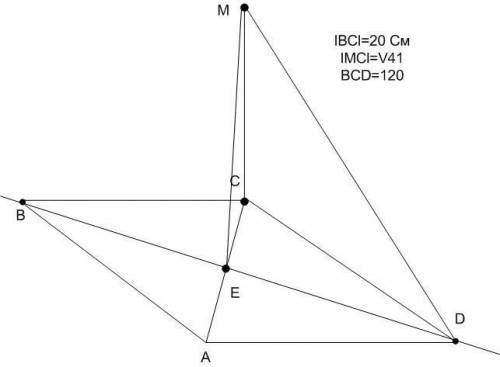
Задача 2. Файл "ромб"
Дано
ABCD - ромб со стороной 20 см
l CD l=20 см
∠BCD=120°
l MC l=√41 см
Найти:
l MD l, l ME l
l MD l=√(l MC l²+ l CD l²);
l MD l=√(√41)²+20²)=√441=21 (см);
Δ CED - прямоугольный, т.к. у ромба диагонали пересекаются под прямым углом.
Сумма углов выпуклого 4-х угольника, а, значит, и ромба - 360°. У ромба противоположные углы равны, значит:
∠CDA=(360°-120-120)/2=60;
Диагональ ромба является биссектрисой противолежащих углов, значит:
∠CDE=∠CDA/2;
∠CDE=60°/2=30°;
В Δ CED l CE l=l CD l*sin(∠CDE);
l CE l=20*sin30°=20*(1/2)=10 (см);
ΔMCE- прямоугольный.
l ME l=√(l CE l²+l MC l²);
l ME l=√(10²+(√41)²)=√141.
ответ: l MD l=21 см, l ME l =√141 см
38= 30+ 8, делятся на 2
48= 30+ 18, делятся на 3
56= 40+ 16, делятся на 4
б) 72= 60+ 12, на 6
65=60+ 15, на 5
96= 80+ 16, на 8
84= 70+ 14, на 7
в) 57= 30+ 27, на 3
76= 40+ 36, на 4
85= 50+ 35, на 5
68= 40+ 28, на 4
г) 148= 100+ 48, на 2
164= 100+ 64, на 2
182= 100+ 82, на 2
246= 200+ 46, на 2
д) 126= 100+ 26, на 2
129= 120+ 9, на 3
120= 90+ 30, на 3
154= 140+ 14, на 7