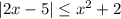Решите модульное неравенство , если можно как можно подробней распишите
ответ:
удастся помешать
пошаговое объяснение:
при выборе произвольного числа n и последующем действии в итоге могут быть получены числа n-1 или n+1, так как они отличаются на 2, а целью собаки является получить число кратное 4, то свинья любое произвольное единичное число может превратить в не кратное 4.
минимальное число чисел которое может задать собака для получения числа кратного 4 является два. это должны быть числа 4*z1 - 1 и 4*z2 + 1 (где z1 и z2 - целые числа). в этом случае как при увеличении, так и при уменьшении на 1, одно из чисел становится кратным 4.
в любой последовательности чисел с четным количеством членов не более половины может быть после действия свиньи кратным 4 (если свинья не поддается), в случае нечетного количества членов, свинья может выбрать действие, которое превращает в не кратные 4 больше половины членов ряда (можно разделить ряд на пары + 1 число и потом произвести над ними одно и то же действие так, что не более одного числа в паре станет кратным 4, а единичное число не будет кратно 4).
в итоге из произвольного ряда чисел (после действия свиньи) кратных 4 может быть получено не более n/2 для рядов с четным количеством членов и не более (n-1)/2 для рядов с нечетным количеством членов
таким образом максимальное количество чисел, кратных 4, которые может получить собака будет равно (2019-1)/2 = 1009
1.
2,8 * (-3,9) - 76,15 : 15,23 = -15,92
1) 2,8 * (-3,9) = -10,92
2) 76,15 : 15,23 = 5
3) -10,92 - 5 = -15,92
ответ: -15,92
2.
34,68 : (7,11 + 1,56) + 46 : (2,45 - 1,65) = 61,5
1) 7,11 + 1,56 = 8,67
2) 34,68 : 8,67 = 4
3) 2,45 - 1,65 = 0,8
4) 46 : 0,8 = 57,5
5) 4 + 57,5 = 61,5
ответ: 61,5
3.
(0,62 + 0,56 - 2,29) * (8,44 - 5,34) = -3,441
1) 0,62 + 0,56 = 1,18
2) 1,18 - 2,29 = -1,11
3) 8,44 - 5,34 = 3,1
4) -1,11 * 3,1 = -3,441
ответ: -3,441
4.
62,93 + (12,5 - 7,6 + 3,21) : 0,1 = 144,03
1) 12,5 - 7,6 = 4,9
2) 4,9 + 3,21 = 8,11
3) 8,11 : 0,1 = 81,1
4) 62,93 + 81,1 = 144,03
ответ: 144,03
(- ∞; -3 ] ∪ [1; + ∞ ).
Пошаговое объяснение:
1. Найдём нули подмодульного выражения:
2х - 5 = 0
2х = 5
х = 2,5
2.
а) Если х ≥ 2,5, то 2х - 5 ≥ 0, l2х - 5 l = 2х - 5 , тогда
l2х - 5 l ≤ х² + 2
2х - 5 ≤ х² + 2
х² + 2 - 2х + 5 ≥ 0
х² - 2х + 7 ≥ 0
(х-1)² + 6 ≥ 0 при всех х из рассматриваемого промежутка, т.е. х ∈ [2,5; + ∞ )
б) Если х < 2,5, то 2х - 5 < 0, l2х - 5 l = - 2х + 5 , тогда
l2х - 5 l ≤ х² + 2
- 2х + 5 ≤ х² + 2
х² + 2 + 2х - 5 ≥ 0
х² + 2х - 3 ≥ 0
(х - 1)(х + 3) ≥ 0
__+__[-3]__-__[1]__+__(2,5)...>
х ∈ (- ∞; -3 ] ∪ [1; 2,5)
Объединим решения, получим
х ∈ (- ∞; -3 ] ∪ [1; 2,5) ∪ [2,5; + ∞ )
х ∈ (- ∞; -3 ] ∪ [1; + ∞ ).
ответ: (- ∞; -3 ] ∪ [1; + ∞ ).