3240
Пошаговое объяснение:
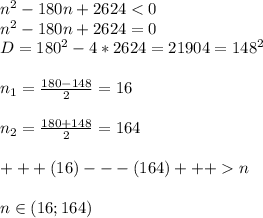
Так как изначальное неравенство строгое, то числа 16 и 164 не включаются и нам не подходят.
Нам нужно найти сумму целых чисел из полученного множества, что делятся на 4, то есть:
20+24+28+32+...+160=?
Это сумма арифметической прогрессии, где
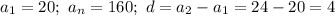
Число членов этой последовательности найдем по формуле n-го члена:
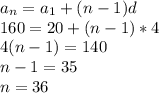
Тогда сумму находим по формуле:
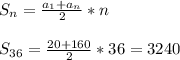
1) Дан развёрнутый угол AOC. По свойству смежных углов, их сумма равна 180°. Вспомним, что градусная мера развёрнутого угла также равна 180°. Также, дан ∠BOC, градусная мера которого 65° (рассуждать можем несколькими но ответ получится один). Чтобы найти ∠AOB, надо из развёрнутого угла AOC вычесть все известные:
∠AOB = ∠AOC - ∠BOC = 180° - 65° = 115° - градусная мера ∠AOB
ответ: ∠AOB = 115°.
2) Дан прямой угол AOC, помним, что его градусная мера равна 90°, и дан ∠BOC, градусная мера которого равна 20°. Чтобы найти ∠AOB, надо из прямого угла AOC вычесть все известные (в нашем случае один):
∠AOB = ∠AOC - ∠BOC = 90° - 20° = 70° - градусная мера ∠AOB.
ответ: ∠AOB = 70°.
3) Дан развёрнутый угол COD (равен 180°), даны два угла: ∠AOC = 60°; ∠BOD = 50°. Чтобы найти ∠AOB, надо из развёрнутого угла AOC вычесть все известные:
∠AOB = ∠COD - ∠AOC - ∠BOD = 180° - 60° - 50° = 180° - (60° + 50°) = 180° - 110° = 70° - градусная мера ∠AOB.
ответ: ∠AOB = 70°.
Если ты нацелена на получение высшего образования, то тебе однозначно следует идти в 11 класс, если же нет, то лучше уйти после 9 класса. В тоже время в 10 и 11 классе у тебя есть ещё два года на то, чтобы немного самоопределиться, даже находясь в 11 классе, я до сих пор не знаю что мне по душе) Просто ищи то, что тебе нравится, мне кажется искать перспективу в будущей профессии неплохо, но в тоже время нужно найти то, что тебе самой нравиться, так как работать всю жизнь на нелюбимой работе - такое себе. Развивайся, найди предметы, которые ты понимаешь и любишь и уже от этого отталкивайся, удачи!)
3240
Пошаговое объяснение:
Чтобы решить неравенство,сначала найдем корни, приравняв его к нулю
По теореме Виета:
Данному условию соответствуют корни 164 и 16
Получается что решением неравенства является отрезок 16<n<164
В этом отрезке следующие числа делятся на 4 без остатка:20,24,28,32,36,40,44,48,52,56,60,64,68,72,76,80,84,88,92,96,100,104,108,112,116,120,124,128,132,136,140,144,148,152,156,160
Посчитаем сумму с арифметической прогрессии