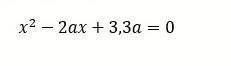
-0,25
Пошаговое объяснение:
x²-2ax+3,3a = 0
Выразим дискриминант, а затем и корни через a:
D = k²-AC = (-a)²-1·3,3a = a²-3,3a (здесь k = B/2)

Для того чтобы найти значения параметра, при которых сумма квадратов вещественных корней была бы равна 1,9, достаточно решить уравнение x_1²+x_2² = 1,9 или
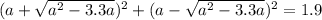
Область допустимых значений (ОДЗ):
a²-3,3a ≥ 0, a(a-3.3) ≥ 0
+ - +
¯¯¯¯¯¯¯¯¯¯(0)¯¯¯¯¯¯¯¯¯¯(3,3)¯¯¯¯¯¯¯¯¯¯
a ∈ (-∞; 0] ∪ [3,3; +∞)
Раскроем скобки и сведем подобные:

D = k²-AC = (-3,3)²+4·1,9 = 10,89+7,6 = 18,49 (опять же k = B/2)

Корень 1,9 не входит в ОДЗ.
Получили, что только одно значение a — -0,25 — удовлетворяет условию.
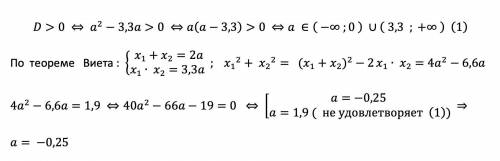
Сначала распишем все формулы и тогда будем вычислять пошагово.
Формула площади боковой поверхности: 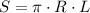
Формула площади полной поверхности: 
Также формула площади полной поверхности:  .
.
1) Площадь основания считается проще некуда, так как площадь полной поверхности - это сумма площади боковой поверхности и площади основания.
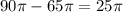 cм².
cм².
2) Отсюда считаем радиус основания:
 . Радиус основания конуса равен 5 см.
. Радиус основания конуса равен 5 см.
3) Вычисляем образующую:
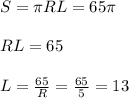 cм. Образующая равна 13 см.
cм. Образующая равна 13 см.
4) Высоту вычислить ещё проще. Конус образуется вращением прямоугольного треугольника вокруг его катета (высоты). Высоту можно было бы вычислить по теореме Пифагора, но в этом нет необходимости, так как в данном случае присутствует египетский треугольник с катетами 5 см и 12 см и гипотенузой 13 см (в данном случае гипотенуза это образующая). Высота равна 12 см.
5) Объём конуса вычисляется по формуле: 
В данном случае число 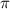 мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с
мы трогать не будем, так как площади боковой и полной поверхностей представлены в форме с
 см³.
см³.
-0,25
Пошаговое объяснение: