Question

Докажите, что для любого натурального числа x, не делящегося ни на 2, ни на 5, существует натуральное число, куб которого оканчивается на x

Answer 1

Во-первых убеждаемся, что при возведении в куб всех 10 однозначных чисел, среди последних цифр получившихся чисел нет повторов (и тем самым. если x однозначное число, задача решена, тут даже ограничения делать не надо). Пусть x   двузначное число, оканчивающееся на 1, или 3, или 7 или 9. Соответственно число, которое мы ищем, будет оканчиваться на 1, или 7, или 3 или 9. Очевидно, для подбора нужного числа достаточно ограничиться поиском среди двузначных чисел, так как следующие разряды при возведении в куб не повлияют на число десятков и единиц куба. Докажем, что если мы возьмем два различных двузначных числа, у которых совпадают числа единиц (и это 1, 3, 7 или 9), а различается количество десятков, то при возведении в куб получатся числа, у которых разное количество десятков. Кстати, давайте для простоты душевной позволять себе двузначные числа с нулевым количеством десятков. Говоря по ученому, мы хотим доказать, что эти кубы не могут быть сравнимы по модулю 100. В самом деле, если число (10a+b)³≡(10c+b)³ (mod 100), то

30ab²+b³ ≡30cb²+b³(mod 100); 30ab²≡30cb² (mod 100); ab²≡cb² (mod 10);

а поскольку b выбирается из набора 1, 3, 7, 9 (все эти числа взаимно просты с 10), то a≡c (mod 10)⇒ a=c. Итак, мы доказали, что возводя 40 двузначных чисел нужного вида в куб, мы будем получать числа, у которых две последние цифры образуют числа, каждый раз разные, и все из того же списка из 40 чисел. Это доказывает утверждение для двузначных чисел.

Далее будем действовать по индукции. Если для k-значных чисел, заканчивающихся на 1, 3, 7 или 9 возведение в куб приводит к числам, последние  k цифр которых образуют попарно различные числа, докажем, что то же верно и для (k+1)-значных чисел.

Заметим, что (k+1)-значное число может быть записано в виде суммы k-значного числа B  и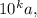 $10^{k}a,$ где  a - однозначное число.

Пусть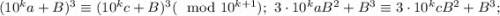 $(10^{k}a+B)^3\equiv (10^{k}c+B)^3 (\mod 10^{k+1});\ 3\cdot 10^kaB^2+B^3\equiv 3\cdot 10^kcB^2+B^3;$

$3\cdot 10^kaB^2\equiv 3\cdot 10^kcB^2 (\mod 10^{k+1});\ a\equiv c(\mod 10)\Rightarrow a=c.$

На этом доказательство завершено.