Question

Найдите все значения параметра а , при каждом из которых наименьшее значение функции f(x) = ax+ |x^2 - 6x + 8| - 4а больше -1

Answer 1

(см. объяснение)

Пошаговое объяснение:

$f(x)=ax+|x^2-6x+8|-4a$

Заметим, что функция непрерывна и на бесконечностях стремится к плюс бесконечности. Тогда она имеет свой минимум при любом значении параметра.

Выполним наложение условия:

$ax+|x^2-6x+8|-4a-1$

Нам надо найти такие значения параметра, чтобы это неравенство было истинно при любом значении переменной $x$.

Откуда перейдем к более удобному виду:

$|x^2-6x+8|+1a(4-x)$

Слева нет параметра. Тогда эту чисть неравенства построим в координатах (x; y), понимая, что она будет фиксирована.

Справа находится параметрическая прямая, вращающаяся вокруг точки (4; 0). Ее тоже строим в той же системе координат.

Тогда задача заключается в том, чтобы сделать так, когда вся левая часть неравенства находится выше прямой.

Покажем соответствующие расположения прямой:

(см. прикрепленный файл)

В первом случае, она касается параболы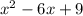 $x^2-6x+9$.

Тогда:

$x^2-6x+9=a(4-x)\\x^2-6x+9-4a+ax=0\\x^2-x(6-a)-4a+9=0\\D=(6-a)^2+4(4a-9)=a^2+4a\\a^2+4a=0\\a=4\\a=0$

Здесь $a=0$ постороннее значение.

Во втором случае, прямая проходит через точку (2; 1).

$1=a(4-2)\\a=\dfrac{1}{2}$

Итого при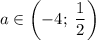 $a\in\left(-4;\;\dfrac{1}{2}\right)$ наименьшее значение функции больше минус одного.

Задание выполнено!