З пункту А в пункт В, відстань між якими 410 км, вирушив автобус. Через 1 годину назустріч йому з пункту В виїхав легковий автомобіль. Знайдіть швидкість автомобіля і автобуса, якщо зустрілися вони через 4 години після початку руху автобуса, і автомобіль їхав зі швидкістю на 20 км/год більшою. Яка відстань буде між ними через 3 години після початку руху легкового автомобіля?( )

👇

Увидеть ответ

Ответ:

annar2001

07.12.2022

Скорость движения автомобиля 70 км/час;

скорость движения автобуса 50 км/час;

расстояние между автобусом и автомобилем через 3 часа после начала движения легкового автомобиля будет равно 0 км.

Пошаговое объяснение:

Задание

Из пункта А в пункт В, расстояние между которыми 410 км, отправился автобус. Через 1 час навстречу ему из пункта В выехал легковой автомобиль. Найдите скорость автомобиля и автобуса, если они встретились через 4 часа после начала движения автобуса, и автомобиль ехал со скоростью на 20 км/ч больше. Какое расстояние будет между ними через 3 часа после начала движения легкового автомобиля?

Решение

1) Пусть х км/час - скорость движения автобуса, тогда (х+20) км/час - скорость движения автомобиля.

Автобус двигался 4 часа, а автомобиль на 1 час меньше, то есть 3 часа. Составим уравнение и найдём х.

4х + 3(х+20) = 410

4х+3х+60 =410

7х = 410-60 = 350

х = 350 : 7 = 50 км/час - скорость движения автобуса.

х+20 = 50 + 20 = 70 км/час - скорость движения автомобиля.

2) Так как автобус и автомобиль встретились через 3 часа после начала движения легкового автомобиля, а к этому времени автобус двигался 4 часа, то расстояние между ними будет:

410 - 50·4 - 70·3 = 410 - 200 - 210 = 0 км

скорость движения автомобиля 70 км/час;

скорость движения автобуса 50 км/час;

4,5(14 оценок)

Открыть все ответы

Ответ:

feliz3600

07.12.2022

Пошаговое объяснение:

1) ОДЗ x-9>0, х>9.

2) На ОДЗ первоначальное уравнение принимает вид:

7x-ln(x-9)⁷-11 = 7x-7ln(x-9)-11

3) Производная суммы равна сумме производных:

(7x-7ln(x-9)-11)' = 7 - 7· (1/(x-9)·(x-9)'-0 = 7 - 7/(x-9)

4) В точке экстремума производная равна нулю:

7 - 7/(x-9) = 0

(7х - 63 - 7) /(х-9) = 0

5) Дробь равна нулю, когда числитель равен нулю:

7х - 63 - 7 = 0

7х = 70

х = 10

6) Исследуем знаки производной:

при 9 < х < 10 у' (9,5) = - 7 <0 - следовательно, функция убывает;

при х > 10 у' (11) = (77 - 63 - 7) / (11 - 9) = 7/2 = 3,5 > 0 - следовательно, функция возрастает; из этого следует, что х = 10 является точкой минимума.

ответ: 10

4,8(58 оценок)

Ответ:

karinohka2006

07.12.2022

Пошаговое объяснение:

первое действие в скобках

1) 1,54+1,18=2,72

дальше по порядку идут действия умножения и деления

2) 54/2,72=9,8529...

разделить 54 на 2,72 ровно нельзя так что переведем в обыкновенную дробь

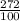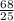
$\frac{272}{100}$ = $\frac{68}{25}$

и повторить деление. Деление дроби равносильно умножение этой же дроби, но перевернутой(числитель стал знаменателем и наоборот)

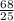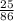
54/ $\frac{68}{25}$ =54* $\frac{25}{86}$

сокращаем 54 и 86 на 2

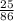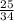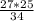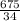
54* $\frac{25}{86}$ =27* $\frac{25}{34}$ = $\frac{27*25}{34}$ = $\frac{675}{34}$

выполнить оставшееся действие. перевести 1,9 в обыкновенную дробь

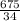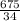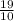
3) $\frac{675}{34}$ - 1,9= $\frac{675}{34}$ - $\frac{19}{10}$

вычесть(там нужно преводить к общему знаменателю, сокращять, но там получаются большие числа, так что мне кажется что вы как то неправильно написали свой вопрос), вычеслить примерное значение

4)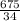 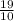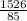$\frac{675}{34}$ - $\frac{19}{10}$ = $\frac{1526}{85}$ ≈18