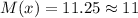Предположим, длина прямоугольника равна A, а ширина прямоугольника равна B.
Площадь S прямоугольника:
S = A * B.
Если длину увеличить на 1, то длина станет равна A + 1,
а если уменьшить ширину на 1, то она станет B - 1.
Площадь S1 этого прямоугольника:
S1 = (A + 1) * (B - 1).
Предположим, что S > S1. Тогда:
A * B > (A + 1) * (B - 1) = A * B - A + B - 1,
0 > - A + B - 1,
A + 1 > B.
Таким образом, мы получили, что если длина прямоугольника увеличенная на 1 мм будет больше ширины, то площадь прямоугольника уменьшится.
в 5а - 36
в 5б - 44
Пошаговое объяснение:
1) так как людей не может быть дробное колличество, то количество учеников 5а класса должно делиться на 9, а 5б на 11
2) будем искать методом подбора:
на 11 делятся только числа: 11, 22, 33, 44, 55, 66, 77(далее уже больше общего количества учеников, что невозможно)
80 - 11 = 69 не делиться нацело на 9, значит не подходит
80- 22=58 не подходит по той же причине
80 - 33 = 47 не подходит по той же причине
80- 44=36 , 36 делится на 9, значит подходит
(далее можешь по такому же принципу проверить все остальные числа делящиеся на 11, но подходящего ответа больше не будет)
итак в 5а - 36 человек
в 5б - 44 человека
Математическое ожидание - сумма попарных произведений значений случайной величины на вероятности, с которыми эти величины достигаются.
То есть, если значение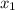 достигается с вероятностью
достигается с вероятностью 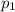 , значение
, значение  - с вероятностью
- с вероятностью  , и так далее, значение
, и так далее, значение 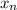 - с вероятностью
- с вероятностью 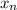 , то математическое ожидание:
, то математическое ожидание:
Математическое ожидание показывает среднее или наиболее вероятное значение случайной величины. В единичном испытании математическое ожидание равно вероятности события.
Для вычисления мат.ожидания как ожидаемого числа вопросов используем формулу:
В нашем случае, - вероятность того, что очередной вопрос не из группы "спринт",
- вероятность того, что очередной вопрос не из группы "спринт", 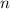 - число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
- число вопросов группы "спринт" (нас интересует сколько раз среди них встретится вопрос не группы "спринт").
Поскольку вопросов не из группы "спринт"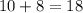 , а общее число вопросов
, а общее число вопросов  , то вероятность того, что очередной вопрос не из группы "спринт" равна:
, то вероятность того, что очередной вопрос не из группы "спринт" равна:
Число вопросов группы "спринт":
Тогда:
Конечно, можно действовать по первой формуле.
Для этого рассмотрим возможные количества вопросов не из группы "спринт", которые могли оказаться в группе "спринт". Это количества: 0, 1, 2, ..., 17, 18.
Найдем вероятности осуществления этих возможностей. Так как общий смысл сохраняется во всех ситуациях, то рассмотрим нахождение вероятности в общем виде - найдем с какой вероятностью i вопросов не из группы "спринт" попадут в группу "спринт".
Число выбрать вопросы в группу "спринт" с учетом этого условия соответствует тому, что из 18 вопросов не группы "спринт" мы выберем некоторые i штук, а остальные (30-i) штук мы выберем из 30 вопросов группы "спринт". Итоговое число благоприятных комбинаций: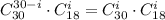 .
.
Общее число выбрать вопросы в группу "спринт" соответствует тому, что из всех 48 вопросов мы выберем некоторые 30 штук. Общее число комбинаций: .
.
Тогда, ситуации, что в группе "спринт" окажется i вопросов не из группы "спринт", соответствует вероятность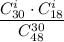 .
.
Запишем математическое ожидание как сумму попарных произведений значений на вероятность:
Можно попробовать упростить эту формулу:
Далее нужно каким-либо досчитать эту величину. Вычисления дают полученный ранее результат:
Учитывая контекст вопроса, а именно, что мат.ожидание соответствует числу вопросов, попавших в группу "спринт", запишем также округленное до целого числа значение мат.ожидания:
ответ: