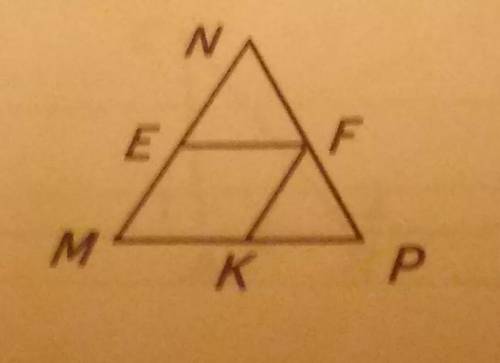
ответ:
f(x) = -x^3+3x^2
1) область определения:
d(f): x принадлежит
2) четность/нечетность:
f(-x) = x^3+3x^2 - не является четной и нечетной
3) непрерывность:
функция непрерывна на всей области определения.
4) точки пересечения с осями координат:
ox: y=0 a(0,0), b(3,0)
oy: x=0 c(0,0)
5) асимптоты:
горизонтальная: нет
наклонная: y = kx+b, - нет
вертикальная: нет, т.к. нет точек разрыва
6) экстремум:
f'(x) = -3x^2+6x = -3x(x-2)
f'(x) = 0 при x = 0 или x = 2
- + -
..>
0 2 x
x=0 - точка минимума f(0) = 0 - наименьшее значение
x = 2 - точка максимума f(2) = 4 - наибольшее значение
7) выпуклость:
f''(x) = -6x+6
f''(x) = 0 при x = 1
+ -
.> x
1
при х график функции имеет выпуклость вниз,
при х - вверх
Пошаговое объяснение:
1) Так как MN параллелен KF, то и ME (является частью стороны MN) параллелен KF. Аналогично, MK параллелен EF.
2) Признак параллелограмма: Если противоположные стороны четырёхугольника попарно параллельны, то четырёхугольник является параллелограммом. Действительно, исходя из первого шага, можно утверждать, что MEFK является параллелограммом.
3) Угол MKF и FKP являются смежными, значит их сумма равна 180. Найдём угол MKF:
∠MKF = 180 ° - ∠FKP = 180 - 54 =126°
4) Свойство: противоположные углы параллелограмма равны. Следует, что ∠MEF = ∠MKF = 126°
5) Свойство четырехугольника MEFK: сумма углов равна 360°, значит ∠MEF+∠EFK+∠MKF+∠KME=360°. Два угла нам известны:
126°+∠EFK+126°+∠KME=360
∠EFK+∠KME=108°
По свойству параллелограмма ∠EFK=∠KME, значит ∠EFK=∠KME=108 / 2 = 54°.