В решении.
Пошаговое объяснение:
1) |5-2х|<-10
↓
5 - 2х < -10 5 - 2x > 10
-2х < -10 - 5 -2х > 10 - 5
-2х < -15 -2x > 5
2x > 15 2x < -5 знак неравенства меняется при делении на минус;
x₁ > 7,5; x₂ < -2,5.
Но х₁ не удовлетворяет второму неравенству, а х₂ не удовлетворяет первому неравенству.
Данное неравенство не имеет решения.
2) |х+2|<3
↓
х + 2 < 3 x + 2 > -3
x < 3 - 2 x > -3 - 2
x₁ < 1; x₂ > -5;
Решения неравенства: х∈(-5; 1).
Неравенство строгое, скобки круглые.
3) |1-2х|≤5
↓
1 - 2х <= 5 1 - 2x >= -5
-2x <= 5 - 1 -2x >= -5 - 1
-2x <= 4 -2x >= -6
2x >= -4 2x <= 6 знак неравенства меняется при делении на минус;
x₁ >= -2; x₂ <= 3;
Решения неравенства: х∈[-2; 3].
Неравенство нестрогое, скобки квадратные.
4) |4х-3|>10
↓
4x - 3 > 10 4x - 3 < -10
4x > 10 + 3 4x < -10 + 3
4x > 13 4x < -7
x₁ > 13/4; x₂ < -7/4;
Решения неравенства: х∈(-∞; -7/4)∪(13/4; +∞).
Неравенство строгое, скобки круглые.
5) |-х+1|>-2,1
↓
-х + 1 > -2,1 -x + 1 < 2,1
-x > -2,1 - 1 -x < 2,1 - 1
-x > -3,1 -x < 1,1
x₁ < 3,1; x₂ > -1,1; знак неравенства меняется при делении на минус;
Решения неравенства: х∈(-1,1; 3,1).
Неравенство строгое, скобки круглые.
95°
Пошаговое объяснение:
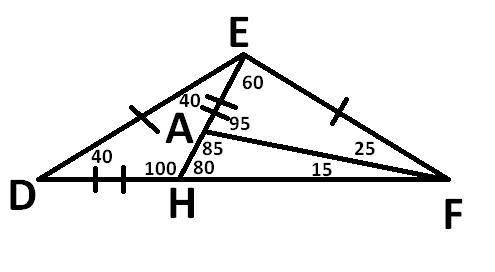
Этот треугольник тупоугольный т.к. ∠DEF=180-40-40=100°;
Мы имеем ∠DFA=15; ∠DEA=40;
Далее эту задачу можно решить двумя :
Первый (Более простой) - ∠AFE=40-∠DFA=40-15=25°; ∠AEF=100-∠DEA=100-40=60°; ∠EAF=180-60-25=95°
Второй (Сложнее, но красивее) - Продолжим прямую EA до соприкосновения с прямой DF в точке H; ∠D=∠DEA=40°; ∠DHE=180-40-40=100°; ∠AHF=180-100=80°; ∠HAF=180-80-∠DFA=180-80-15=85°; ∠EAF=180-85=95°
Кстати, нету смысла писать одно и то же задание несколько раз, от этого всё равно нету толка - тебе в основном только я и отвечаю. Это лишь пустая трата для тебя.
0,6
Пошаговое объяснение:
sin x + cos x = 1,4
sin 5x = sin(2x + 3x)
1) Найдем sin 2x и cos 2x
(sin x + cos x)^2 = 1,4^2
sin^2 x + cos^2 x + 2sin x*cos x = 1,96
1 + sin 2x = 1,96
sin 2x = 0,96
sin^2 (2x) = 0,96^2 = 0,9216
cos^2 (2x) = 1 - sin^2 (2x) = 1 - 0,9216 = 0,0784
cos 2x = √(0,0784) = 0,28
2) Найдем sin x и cos x
cos 2x = 2cos^2 x - 1 = 0,28
2cos^2 x = 1,28
cos^2 x = 1,28/2 = 0,64
cos x = √0,64 = 0,8
sin^2 x = 1 - cos^2 x = 1 - 0,64 = 0,36
sin x = √0,36 = 0,6
3) Найдем sin 3x и cos 3x
sin 3x = sin (x+2x) = sin x*cos 2x + cos x*sin 2x = 0,6*0,28 + 0,8*0,96 = 0,936
sin^2 (3x) = 0,936^2 = 0,876096
cos^2 (3x) = 1 - sin^2 (3x) = 1 - 0,876096 = 0,123904
cos 3x = √0,123904 = 0,352
4) И, наконец, найдем sin 5x
sin 5x = sin (2x + 3x) = sin 2x*cos 3x + cos 2x*sin 3x = 0,96*0,352 + 0,28*0,936 =
= 0,33792 + 0,26208 = 0,6
Как ни странно, оказалось, что sin 5x = sin x