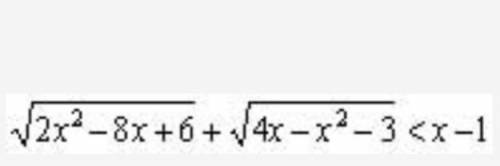
3.
Пошаговое объяснение:
Найдем область допустимых значений. Так как арифметический квадратный корень определен на множестве неотрицательных чисел, то найдем ОДЗ, решив систему неравенств.
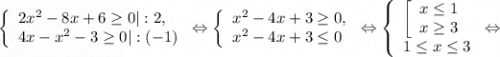
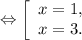
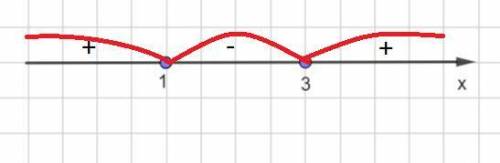
Решим отдельно каждое неравенство методом интервалов.
Рассмотрим функцию 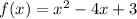
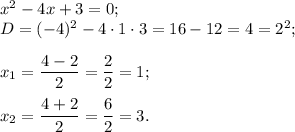
Определим знак функции на каждом интервале и получим:
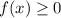 x∈ (-∞; 1]∪[3; +∞)
x∈ (-∞; 1]∪[3; +∞)
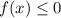 x∈[1; 3]
x∈[1; 3]
Данная системе имеет решение только, если х=1 и х=3.
Проверим каждое значение:
x=1
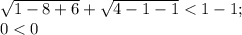
неверно
x=3
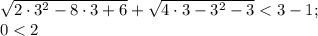
Данное неравенство верно. Значит, решение заданного неравенства является х=3
Обратное утверждение или обратная теорема - это такая формулировка исходной (прямой) теоремы, где условие и заключение переставлены местами.
Прямое утверждение: Каждое число, которое можно представить в виде отношения двух целых чисел, является рациональным.
Обратное утверждение: Число, которое является рациональным, можно представить в виде отношения двух целых чисел.
Да, утверждение является истинным, поскольку все рациональные числа - это как целые числа, так и дроби (которые и являются отношением двух целых чисел).
x = 3
Пошаговое объяснение:
Заменим выражение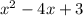 на t, тогда левая часть будет иметь вид
на t, тогда левая часть будет иметь вид
Тогда решаем уравнение t = 0
По теореме Виета легко находятся корни 1 и 3.
При x = 1:
Неравенство принимает вид 0 < 0, что не является верным неравенством.
При x = 3:
Неравенство принимает вид 0 < 2 и это является верным неравенством