
Пошаговое объяснение:
Решение на фото.
В №2 возможно опечатка, так как все слагаемые с буквами удаляются, поэтому нельзя подставить b= –5. При любых значениях b результат выражения
будет 8. Подставим значение b= –5:
(2–b)³+b(b²–6b+12)=
=(2–(–5))³+(–5)((–5)²–6×(–5)+12)=
=(2+5)³+(–5)(25+30+12)=343+(–5)×67=
=343–335=8
ОТВЕТ: 8
В этом номере при решении в тетради использована формула куба разности:
(а–b)³=a³–3a²b+3ab²–b³
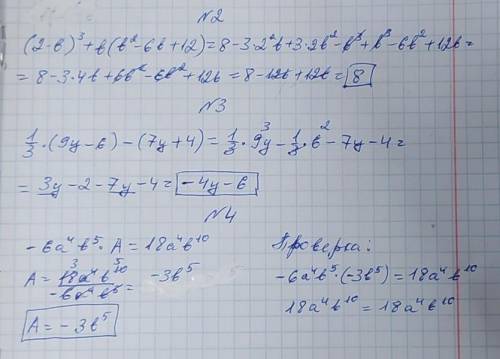
это решение системы
х²-5х+6>0; х²-5х+6=0; по теореме, обратной теореме ВИЕТА, находим корни уравнения х=2;х=3, значит, х²-5х+6=(х-2)(х-3), тогда
(х-2)(х-3)>0
(2-x)/(x-3)≥0⇒(x-2)/(x-3)≤0
второе неравенство равносильно системе
(x-2)(x-3)≤0;
х≠3
Т.о., для решения вопроса области определения данной функции надо решить такую систему
(х-2)(х-3)>0
(x-2)(x-3)≤0;
х≠3
как видим, одновременно произведение (х-2)(х-3) и быть большим или равным нулю и быть меньшим нуля при х≠3, быть не может. поэтому данная функция не определена ни при каких значениях х.
2) не совсем поняла,извиняй
3) -4y-6
4) 18a^4b^10