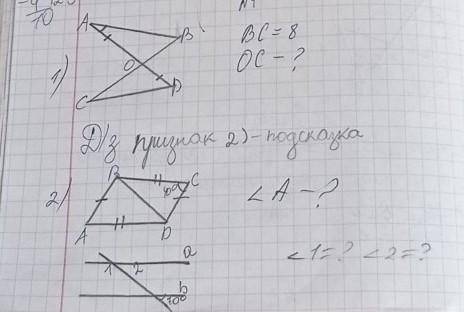
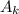Математика: 3 задачи решить буду очень благодарна

3 задачи решить буду очень благодарна

👇

Ответ:

nik123red

07.08.2020

1.BC=ОС+ОВ,значит ОС=8:2=4

2. угол А=углу С тк при наложении треугольников они совпадут и тогда будет 1 признак равенства треугольников(2 стороны и 1 угол)

3. угол который равен 70 градусов и угол 2 являются односторонними поэтому,угол 2=180°-70°=110°. угол 1 и 2 являются смежными значит угол 1=180°-110°=70°

4,7(7 оценок)

Открыть все ответы

Ответ:

Xcalibur

07.08.2020

Если выражаться строго математически, то мы имеем дело со схемой испытаний Бернулли со следующими вероятностями событий:
p = P(попадание)=1 - P(промах) = 1 - 0,4 = 0,6
q = P(промах) = 0,4

В рамках данной модели испытаний вероятность успешного события A_k

(т.е. вероятность того, что произойдёт в точности

успехов из

), подчиняется биномиальному распределению:
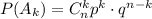$P(A_k) = C_n^k p^k \cdot q^{n-k}$ , где
символ C_n^k

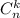означает число выбрать из

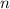элементов

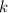элементов без учёта порядка. Известно, что
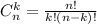$C_n^k = \frac{n!}{k! (n-k)!}$ .

а) Вероятность того, что ровно 7 пуль из 10 попали в цель, составляет
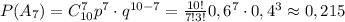
$P(A_7) = C_{10}^7 p^7 \cdot q^{10-7} = \frac{10!}{7! 3!} 0,6^7 \cdot 0,4^3 \approx 0,215$

б) Для того, чтобы найти вероятность того, что хотя бы одна пуля попала в цель, нужно понимать, что множество всевозможных событий $\Omega$ состоит из двух непересекающихся множеств-альтернатив: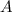

- есть хотя бы одно попадание;
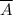$\overline{A}$ - нет ни одного попадания.
Из определения вероятности (как числовой функции множеств) немедленно следует, что
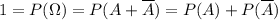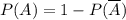$1 = P(\Omega) = P(A + \overline{A}) = P(A) + P(\overline{A})$ , поэтому интересующая нас вероятность выражается следующим равенством: $P(A) = 1 - P(\overline{A})$ .

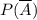Теперь осталось лишь найти вероятность непопадания $P(\overline{A})$ . Можно действовать по общей формуле вероятностей в схеме испытания Бернулли (и получить тот же самый результат!), но в данном случае ситуация упрощается, если напрямую воспользоваться независимостью испытаний: вероятность непопадания в серии из 10 выстрелов равна произведению вероятностей непопадания после 1-го выстрела, после 2-го выстрела и т.д., до 10-го выстрела:
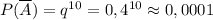$P(\overline{A}) = q^{10} = 0,4^{10} \approx 0,0001$ ,
поэтому вероятность того, что хотя бы одна пуля попала в цель, равна
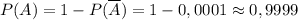
$P(A) = 1 - P(\overline{A}) = 1 - 0,0001 \approx 0,9999$

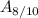в) Событие $A_{8/10}$ "не менее 8-ми пуль попали в цель" является суммой трёх взаимоисключающих событий A_8

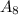"ровно 8 из 10 пуль попали в цель", A_9

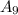"ровно 9 из 10 пуль попали в цель" и 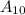$A_{10}$ "ровно 10 из 10 пуль попали в цель", поэтому искомая вероятность равна: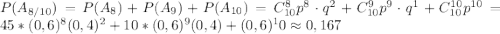
$P(A_{8/10}) = P(A_8) + P(A_9) + P(A_{10}) = C_{10}^{8}p^8 \cdot q^2 + C_{10}^{9}p^9 \cdot q^1 + C_{10}^{10} p^{10} = 45*(0,6)^8(0,4)^2 + 10*(0,6)^9(0,4) + (0,6)^10 \approx 0,167$

ответ: а) 0,215 б) 0,9999 в) 0,167.

4,7(55 оценок)

Ответ:

ArtemD98

07.08.2020

Задача № 1
1) переведем м в км: 41 км=41000 м
2) На сколько метров длина береговой линии Нарочи больше его глубины (чтобы посчитать "НА СКОЛЬКО" - необходимо выполнить действие вычитание):
41000-24=40976 (м)
ответ: длина береговой линии Нарочи больше его глубины на 40976 метров.

Задача №2
Условия задачи: Площадь полей равна 500 га. Кукуруза занимает 1/5 часть площади этих полей , а свёкла - 1/10. Какая площадь полей не засеяна?
1) 500*1/5=100 (га) - занимает кукуруза.
2) 500*1/10=50 (га) - занимает свекла.
3) 100+50=150 (га) - засеяны кукурузой и свеклой.
4) 500-150=350 (га) - не засеяна.
ответ: 350 гектар не засеяны ничем.

4,4(83 оценок)

Это интересно:

Стиль-и-уход-за-собой

17.12.2021

Горячее масло: идеальный способ привести ваши волосы в порядок?...

Компьютеры-и-электроника

10.11.2021

Как изменить список программ для автозапуска...

Кулинария-и-гостеприимство

31.12.2020

Как приготовить пасту Чикен Альфредо, чтобы она получилась вкусной?...

Дом-и-сад