Пошаговое объяснение:
1-Как вычислить высоту конуса, зная образующую и радиус основания?
Образующая конуса, высота и радиус основания образуют прямоугольный треугольник.
Поэтому если известна образующая (гипотенуза) и радиус (катет), то высоту можно выразить с теоремы Пифагора.
a² = c² - b², a = √(c² - b²).
a - высота, b - радиус, c - образующая.
2- Ребро куба равно 3 см. Найти объем и площадь полной поверхности куба.
Прямоугольный параллелепипед, все грани которого - квадраты, называется кубом.
Все ребра куба равны, а площадь поверхности куба равна сумме площадей шести его граней, т.е. площади квадрата со стороной H умноженной на шесть.
Площадь поверхности куба равна: S = 6 · H², где (H - высота ребра куба).
S = 6 · 3² = 6 * 9 = 54 см².
Объем куба равен кубу его ребра: V=H³, где H - высота ребра куба.
V= 3³ = 27 см³.
3- Длина, ширина и высота прямоугольного параллелепипеда соответственно равны: 2см, 3см, 1см. Найти объем и площадь полной поверхности параллелепипеда.
Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипед имеет шесть граней, и все они — параллелограммы.
Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым.
Прямой параллелепипед у которого все шесть граней прямоугольники, называется прямоугольным.
Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:
S = 2 · (Sa + Sb + Sc) = 2 · (ab + bc + ac), где
a – длина, b – ширина, c – высота параллелепипеда.
S = 2 * (2*3 + 3*1 + 2*1) = 2 * (6 + 3 + 2) = 2 * 11 = 22 см²
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
V= SH= a·b·c, где
H - высота параллелепипеда, где a – длина, b – ширина, c – высота параллелепипеда.
V= 2 * 3 * 1 = 6 см³
4- Длина каждого ребра правильной треугольной пирамиды равна 8 см. Высота пирамиды равна 6 см. Найти площадь полной поверхности и объем пирамиды.
Правильная треугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный треугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
У правильной треугольной пирамиды в основании лежит равносторонний треугольник со сторонами a, и три боковые грани — равносторонние треугольники с основанием а и бедрами а.
Площадь правильной треугольной пирамиды равна сумме площадей ее основания и трех боковых граней.
S = Sосн + 3•Sбок
Используя формулы площади равностороннего треугольника получим:
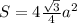
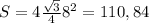 см²
см²
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S на высоту h.
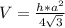 , где
, где
a — сторона правильного треугольника - основания правильной треугольной пирамиды.
h — высота правильной треугольной пирамиды
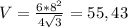 см3
см3
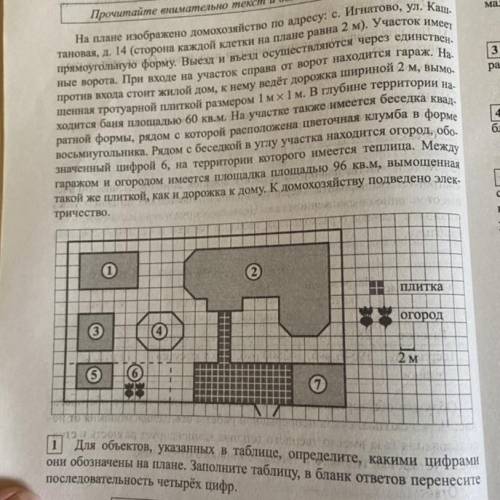
Клумба - 4, Баня - 1 , Беседка - 3, Теплица - 5
Пошаговое объяснение:
По клумбе - на рисунке один восьмиугольник, он обозначен 4.
По бане - это самое большое строение в глубине (кроме дома), его ширина 6 м.(3 клетки), длина 10 м.(5 клеток). Значит площадь строения 6*10=60 кв.м.
По беседке - она рядом с клумбой, а там только один объект рядом с клумбой.
По теплице - на территории огорода только один объект, обозначенный цифрой 5 (цифрой 6 обозначен сам огород).