Из данного задания следует, что необходимо написать разность двух выражений и упрости её:-5-k и27,1+k . То отнимаем от - 5 - k выражение 27,1 + k, в результате получается следующее решение :
( - 5 - k ) - ( 27,1 + k)
Далее открываем скобки, и так как перед второй скобкой стоит знак минус, значит меняем знаки чисел, которые находятся в скобке, на противоположные в результате получается следующее :
( - 5 - k ) - ( 27,1 + k ) = - 5 - k - 27,1 - k =
Далее упрощаем выражение, складывая отрицательные числа , в результате получается следующее
- 5 - k - 27.1 - k = - 2 k - 32,1.
Пошаговое объяснение:
70 км /ч
Пошаговое объяснение:
Таблица:
V S t
Двухэтажный автобус x км/ч 630 км 630/ x ч.
Микроавтобус (x+20)км/ч 630 км 630 / (x+20) ч.
Пояснение к таблице
Шаг 1 Т.к. время прибывания двух автобусов с разницей 2 часа,то пусть t д. - время двухэтажного автобуса ; t м. - время микроавтобуса :
t д. - t м. = 2 часа
Шаг 2 Далее, пусть x км/ч - скорость двухэтажного автобуса . Так как микроавтобус был быстрее на 20 км/ч ,то (x+20) км/ч - скорость микроавтобуса.
Шаг 3 Т.к. общее расстояние 630 км ,то время каждого автобуса можно выразить через формулу: t = S:V и получаем
t д. = 630/ x
t м. = 630 / (x+20)
Шаг 4 Подставим данные из шага 3 в выражение t д. - t м. = 2 часа
630/x - 630 /(x+20) = 2
Шаг 5 Решаем уравнение 630/x - 630 /(x+20) = 2
630/x - 630 /(x+20) = 2
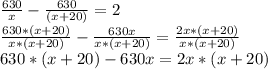
После преобразования получаем:
2x² +40*x - 12600 = 0
x² +20*x - 6300 = 0
D = b² - 4ac = 25600
x1,2 = - b ± √D /2a = -20 ± 160 /2
x1 = 70
x2 ≠ - 90 - не подходит,т.к. скорость не может быть отрицательной!
ответ: Скорость двухэтажного автобуса 70 км /ч
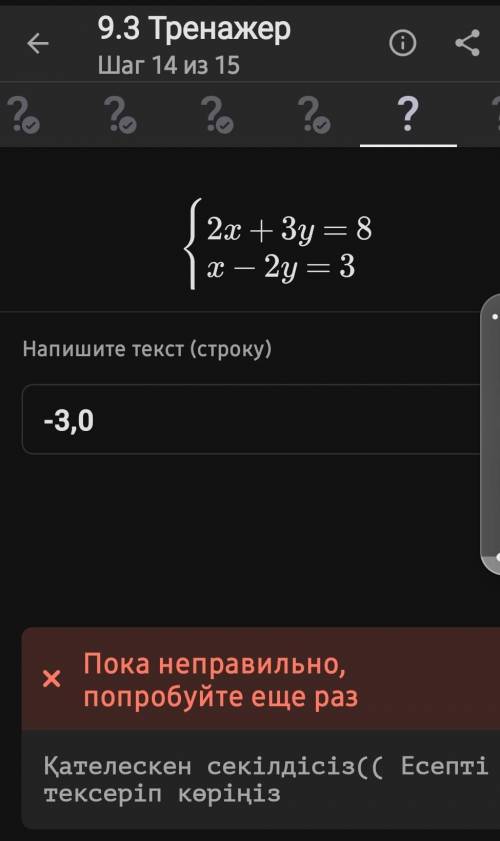
2x + 3y = 8
x - 2y = 3
x = 3 + 2y
2(3 + 2y) + 3y = 8
6 + 4y + 3y = 8
7y = 2
y = 2/7
x = 3 + 2*2/7 = 3 4/7 = 25/7
ответ (25/7, 2/7)