
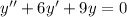
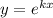 .
.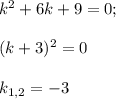
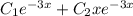
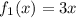 и
и 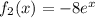
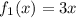
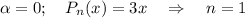
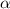 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.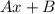
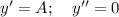 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 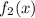 .
.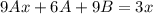
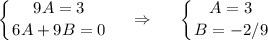
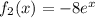
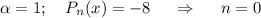
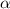 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: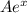
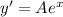 и
и 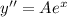
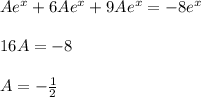
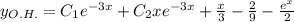
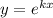 .
.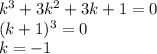
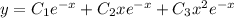
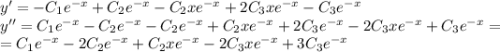
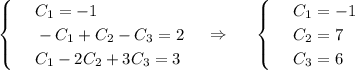
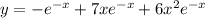
1) > так как 1 км это 1000 м, в этом случае 4,5 км это 4500 м, что больше, чем 4050 м
2) =, так как 1ц это 100 кг, в этом случае 4,5 ц это 450 кг, что больше чем 405 кг
3) =, так как 1 дм это 10 см, в этом случае 4 дм это 40 см
4) >, так как 1 мм² это 0,1 см², в этом случае 4000мм² это 40 см²