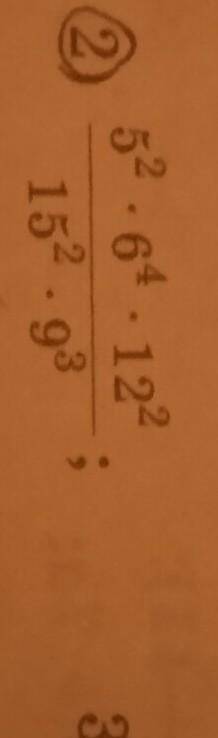
ответ: 256/9
Пошаговое объяснение:
пользуйся это правильно (◡‿◡✿)


Даны две параболы y = x^2 + 4 и y = -(6 - x)^2 - 2, имеющие две общие касательные. Найти абсциссу точки пересечения этих касательных между собой.
Уравнение касательной - это уравнение прямой и имеет вид y=kx+b
Общая касательная пересекается с каждым графиком в одной точке. Тогда для первого графика точку пересечения с касательной можно найти из уравнения x2 + 4 = kx + b, для второго графика из уравнения –(6 –x)2- 2 = kx + b.
1) x2 + 4 = kx + b
x2+ 4 – kx - b = 0
x2 – kx + (4 - b) = 0
Касательная имеет с графиком только одну общую точку, следовательно, корень уравнения должен быть один, а это возможно, когда дискриминант равен нулю.
D = k2 - 4(4 - b) = 0
2) –(6 –x)2- 2 = kx + b.
-36 + 12x - x² - 2 = kx + b
x2 - (12 - k)x + (38 + b) = 0
Приравниваем дискриминант к нулю:
D = (12 - k)2 - 4(38 + b) = 0.
Так как касательная общая, значит, дискриминанты обоих уравнений должны быть равны нулю вместе. Решаем систему уравнений:
{ k2 - 4(4 - b) = 0;
{ (12 - k)2 - 4(38 + b) = 0.
{ k2 – 16 + 4b = 0;
{ 144 - 24k + k2 – 152 - 4b = 0.
{ k2 + 4b - 16 = 0;
{ k2 – 24k - 4b - 8 = 0.
Вычтем почленно из первого уравнения второе:
24k + 8b - 8 = 0 или, сократив на 8,
3k + b - 1 = 0.
b = 1 - 3k. Подставим в первое уравнение:
k2 + 4(1 - 3k) - 16 = 0,
k2 - 12k + 4 - 16 = 0,
k2 - 12k - 12 = 0. D = 144 – 4*1*(-12) = 192,
k1 = (12 - √192)/2 = (12 - 8√3)/2 = 6 - 4√3 ≈ -0,9282,
k2 = (12 + √192)/2 = (12 + 8√3)/2 = 6 + 4√3 ≈12,9282,
b1 = 1 - 3·(6 - 4√3) = -17 + 12√3 ≈ 3,7846,
b2 = 1 - 3·(6 + 4√3) = -17 - 12√3 ≈ -37,7846.
Решение состоит из двух пар чисел:
(k = 6 - 4√3; b = -17 + 12√3) и (k = 6 + 4√3; b = -17 - 12√3).
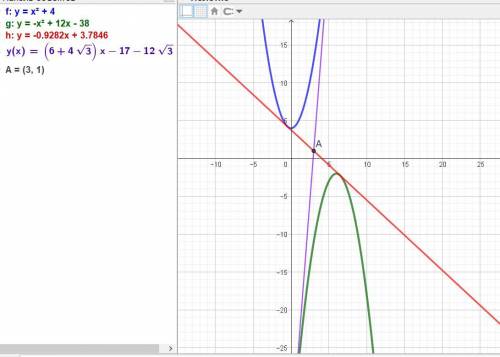
Это означает, что графики имеют две общие касательные, уравнения которых:
y = (6 - 4√3)x -17 + 12√3 и у = (6 + 4√3)x -17 - 12√3.
Находим точку А пересечения касательных.
(6 - 4√3)x -17 + 12√3 = (6 + 4√3)x -17 - 12√3,
6x - 4√3x - 6x - 4√3x = -17 - 12√3 +17 - 12√3,
- 8√3x = - 24√3,
x = 3, y = (6 - 4√3)*3 -17 + 12√3 = 18 - 12√3 -17 + 12√3 = 1.
ответ: точка пересечения А(3; 1).
Есть небольшая история про Декартову плоскость
Давно в Англии, во времена когда все очень любили ходить в театры существовала такая проблема
Большая давка и множество конфликтов за место в театре, бывали даже смертельные случаи
Проблема решилась благодаря Рене Декарту, который изобрел координатную плоскость, и именно благодаря ему появилась нумерация рядов и кресел в театрах, данная система используется по сей день
Если провести аналогию, то покупая билет в кинотеатр, то на билете указаны координаты точки(места) в зале
Надеюсь ребенок поймет, в кино много кто ходил)
256
_
9
Десятичный вид:
28.¯4
В форме смешанного числа:
28 4
_
9