Даны точки A(-4;2;-1), B(1;2;1) и C(-2;0;1).
Если плоскость перпендикулярна вектору BC, то этот вектор и есть нормальным вектором плоскости.
Находим вектор ВС.
ВС = (-2-1; 0-2; 1-1) = (-3; -2; 0).
У параллельной прямой коэффициенты общего уравнения плоскости Ax + By + Cz + D = 0 равны координатам нормального вектора.
Подставив координаты точки А(-4;2;-1), получаем уравнение:
-3*(x + 4) + (-2)*(y - 2) + 0*(z + 1) = 0,
-3x - 12 - 2y + 4 = 0,
-3x - 2y - 8 = 0 или с положительным знаком при х:
3x + 2y + 8 = 0.
Функция не чётная , ни нечетная
f(-x)=36x×(x+1)³
Производная:
y'=d/dx(36x⁴-108x³+108x²-36x)
используем правило дифференцирования
переписуем такой же самый пример как на вверху подставляя в начале y'=36×4x³
y'=36×4x³-108+3x²+108×2x-36
ответ : y'=144x³-324x²+216x-36
Область определения: x-1
точка перегиба:
y'=144x³-324x²+216x-36
y"=432x²-648x+216
решаем уравнения
0=432x²-648x+216
определяем интервалы
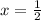
x=1
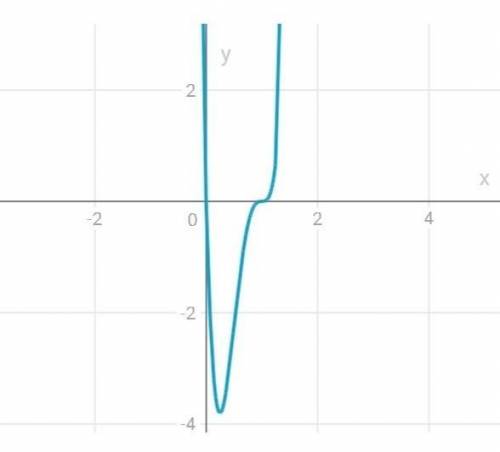
y=36x×(x-1)³, x=1/2
y=36x×(x-1)³ , x=1
Точки перегиба:
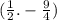
(1,0)
асиптоты:
lim x>+бесконечность (36x×(x-1)³)
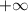
функция не имеет горизонт асиптот
наклоных тоже самое
не имеет
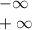
функция многочлен
сделал все что смог
По течению реки теплоход пройдёт 68,9 км против течения 101,2 км
Пошаговое объяснение:
Скорость теплохода - 25,3 км/ч
Скорость течения реки - 1,2 км/ч
Скорость теплохода по течению реки 25,3+1,2=26,5 км/ч
Скорость теплохода против течения реки 25,3-1,2 =24,1 км/ч
1) 26,5*2,6=68,9(км теплоход за 2,6 часа по течению реки
2) 25,3*4=101,2(км теплоход за 4 чеса против течения реки