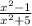
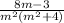
1). Все одиннадцатиклассники из этой школы ростом больше 180 см, поэтому ростом в 173 см они быть никак не могут. Неверно.
2). В условии написано, что каждый одиннадцатиклассник ростом меньше 195 см. Поэтому это утверждение верно.
3). Опять же, все одиннадцатиклассники в этой школе не доросли даже до 196 см, не то что до 197. Утверждение неверно.
4). Так как рост учеников 11 класса этой школы колеблется в пределах 180-195 см (невключая 180 и 195), то разница будет меньше 195-180=15 см. Верно.
Вот мы и разобрали все утверждения. Из них верными оказались только два - №2 и №4.
1). Все одиннадцатиклассники из этой школы ростом больше 180 см, поэтому ростом в 173 см они быть никак не могут. Неверно.
2). В условии написано, что каждый одиннадцатиклассник ростом меньше 195 см. Поэтому это утверждение верно.
3). Опять же, все одиннадцатиклассники в этой школе не доросли даже до 196 см, не то что до 197. Утверждение неверно.
4). Так как рост учеников 11 класса этой школы колеблется в пределах 180-195 см (невключая 180 и 195), то разница будет меньше 195-180=15 см. Верно.
Вот мы и разобрали все утверждения. Из них верными оказались только два - №2 и №4.
дробь имеет смысл, когда знаменатель не равен нулю
1. приравняем знаменатель к нулю
x^2+5=0
x^2=-5 - нет действительных корней, значит x ∈ R
2. m^2(m^2+4)=0
m=0=> m≠0
m^2=-4 - нет действительных корней
m ≠ 0
m ∈ (-∞; 0) ∪ (0; +∞)
Пошаговое объяснение: