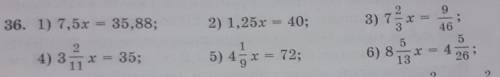
Сторона АВ треугольника АВС лежит в плоскости альфа.Плоскость бетта параллельна плоскости альфа и пересекает стороны АС и ВС в точках А1 и В1 соответственно.Найти длину отрезка А1В1,если АВ=12 см,СВ1:В1В=2:3
Объяснение:
По условию СВ1:В1В=2:3 ⇒на СВ приходится 5 частей.
α║β , то линии пересечения плоскостей параллельны ⇒АВ║А₁В₁.
ΔАВС подобен ΔА₁В₁С по 2 углам : ∠АВС=∠А₁В₁С как соответственные СВ-секущая, ∠С-общий .Поэтому сходственные стороны пропорциональны \frac{AB}{A1B1} =\frac{BC}{B1C}
A1B1
AB
=
B1C
BC
или \frac{12}{A1B1} =\frac{5}{2}
A1B1
12
=
2
5
или А₁В₁= \frac{24}{5}
5
24
=4,8
Найдем значение выражения - a * b * a + a ² * b × 2 * a * b + 4 при a = 2, b = ½.
Для того, чтобы найти значение выражения, нужно известные значения подставить в само выражение и вычислить его значение. То есть получаем:
- a * b * a + a ² * b × 2 * a * b + 4 = - 2 * 1/2 * 2 + 2 ^ 2 * 1/2 * 2 * 2 * 1/2 + 4;
Сначала в порядке очереди вычисляем умножение или деление, потом проводятся действия сложения или вычитания. То есть получаем:
- 2 * 1/2 * 2 + 2 ^ 2 * 1/2 * 2 * 2 * 1/2 + 4 = - 2 + 4 + 4 = 2 + 4 = 6.
Пошаговое объяснение:
1) 7,5x = 35,88
х= 35,88 : 7,5
х= 4,784
2) 1,25x = 40
х=40 : 1,25
х= 32
3)7 2/3x=9/46
23/3х=9/46
х= 9/46 * 3/23
х= 27/1058
4) 3 2/11х= 35
35/11х= 35
х=35 *11/35
х=11
5) 4 1/9 x = 72
х= 72 : 37/9
х= 72 *9/37
х= 648/37
х= 17 19/37
6) 8 5/13х= 4 5/26
109/13х= 109/26
х= 109/26 * 13/109
х= 1/2