1) Область определения функции у = 2 - 1/х:
(-∞; 0) ∪ (0; +∞)
2) Область определения функции у = 2 - 1/(х-2):
(-∞; 2) ∪ (2; +∞)
Пошаговое объяснение:
1) Область определения функции у = 2 - 1/х:
х - любое, кроме х = 0, т.к. на ноль делить нельзя.
ОДЗ: х ≠ 0.
То же, в математических символах:
(-∞; 0) ∪ (0; +∞)
2) Область определения второй функции:
х - любое, кроме х = 2, т.к. в этом случае знаменатель превращается в ноль, а на ноль делить нельзя.
ОДЗ: х ≠ 2.
То же, в математических символах:
(-∞; 2) ∪ (2; +∞)
3) Графики функций по схеме преобразования - в прикреплении:
по п. а) - 3 графика;
по п. б) - 4 графика.
Построение каждого графика сопровождается комментариями: как последовательно из гиперболы были построены графики заданных функций. В прикреплении один и тот же файл дан и в WORD'e, и в PDF, т.к не знаю, какой из них у Вас лучше откроется.
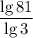1) По формуле перехода к новому основанию 
в данном случае а = 3, b = 81, c = 10
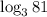
3) Вынесем степень как множитель 
в данном случае а = 3, b = 3, c = 4
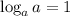
в данном случае а = 3
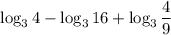1) По формуле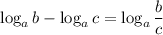 
в данном случае а = 3, b = 4, c = 16
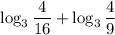
в данном случае а = 3, b =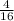 
, с = 
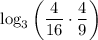
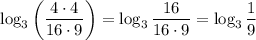4) Заменим 
на 3⁻²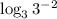
5) Вынесем степень как множитель в данном случае а = 3, b = 3, c = -2
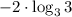
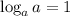
в данном случае а = 3
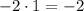
1) Занесем множитель как степень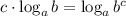 
в данном случае c = 2, a = 7, b = 27
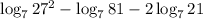
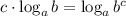
в данном случае c = 2, a = 7, b = 21
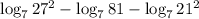
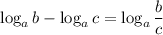
в данном случае а = 7, b = 27², c = 81
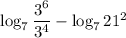
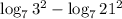6) По формуле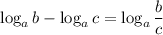 в данном случае а = 7, b = 3², c = 21²
8) Заменим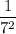 
на 7⁻²
в данном случае а = 7, b = 7, c = -2
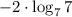
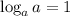
в данном случае а = 7
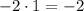
Пошаговое объяснение: