
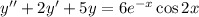
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
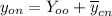
Составим однородное дифференциальное уравнение, соответствующее данному неоднородному:
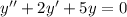
Составим характеристическое уравнение и решим его:
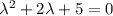
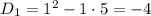
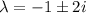
Общее решение однородного уравнения:
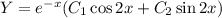
Запишем в общем виде частное решение данного неоднородного уравнения, учитывая, что в правой части стоит произведение экспоненты и на косинус, а также то, что степень экспоненты и выражение под знаком косинуса совпадают с соответствующими выражениями, полученными при решении однородного уравнения:
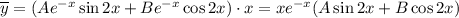
Находим первую производную:
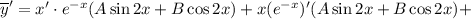
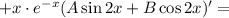
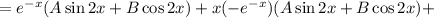
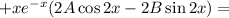
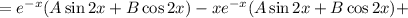
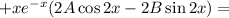
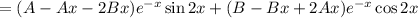
Находим вторую производную:
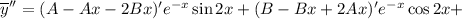
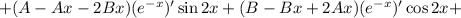
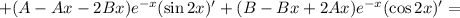
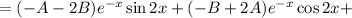

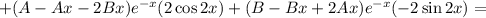
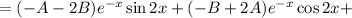
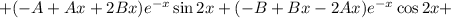
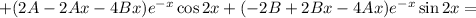
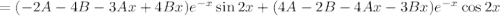
Подставляем в исходное уравнение:
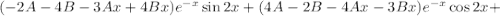
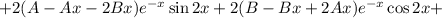
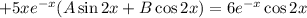
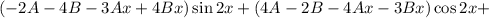
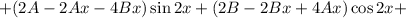
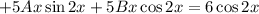
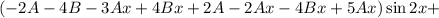
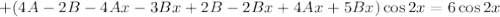
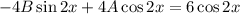
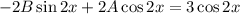
Условие равенства левой и правой частей:
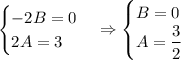
Частное решение данного неоднородного уравнения:
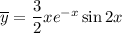
Общее решение данного неоднородного уравнения:
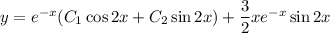
Найдите значение выражения: 8a-2b(3a-4),если a+b=1/4;ab=-1/6
1.раскроем скобки,затем сгруппируем, получится: 8a-2b(3a-4) = 8a-6ab+8b =8(a+b)-6ab
2. подставляем: 8*1/4 - 6*(-1/6) = 3
Решите систему неравенств: {2x-4≥3x+1 5x+5≤4x+3
1. система {2x-4≥3x+1 5x+5≤4x+3 ;
2x-4≥3x+1 5x+5≤4x+3
2х-3х≥1+4 5х-4х ≤3-5
-х≥5 х≤-2
х≤-5
ответ: х принадлежит ( -бесконечности; 5]