ответ:длинна 27дм, периметр 78дм,324 дм2(в квадрате)площадь
Пошаговое объяснение:15+12=27 дм длинна
12+12+27+27=24+54=78дмипериметр
27×12=324дм2(в квадрате) площадь
a) \frac{3}{2 \sqrt{7} } = \frac{3 \times \sqrt{7} }{2 \times \sqrt{7 \times }\sqrt{7} } = \frac{3}{2 \times 7} = \frac{3}{14}a)
2
7
3
=
2×
7×
7
3×
7
=
2×7
3
=
14
3
\begin{gathered}b) \frac{9}{7 + 4 \sqrt{3} } = \frac{9 \times (7 - 4 \sqrt{3} )}{(7 + 4 \sqrt{3} ) \times (7 - 4 \sqrt{3} )} = \frac{63 - 36 \sqrt{3} }{ {7}^{2} -{ (4 \sqrt{3}) }^{2} } = \\ = \frac{63 - 36 \sqrt{3} }{49 - 16 \times 3} = \frac{63 - 36 \sqrt{3} }{49 - 48} = \frac{63 - 36 \sqrt{3} }{1} = 63 - 36 \sqrt{3}\end{gathered}
b)
7+4
3
9
=
(7+4
3
)×(7−4
3
)
9×(7−4
3
)
=
7
2
−(4
3
)
2
63−36
3
=
=
49−16×3
63−36
3
=
49−48
63−36
3
=
1
63−36
3
=63−36
3
ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
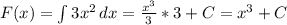
Подставляем в первообразную границы интегрирования:

2.
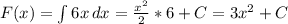
Подставляем в первообразную границы интегрирования:
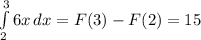
3.

Подставляем в первообразную границы интегрирования:
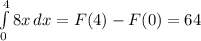
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
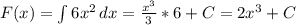
Подставляем в первообразную границы интегрирования:
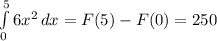
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

16+12=28(дм)- длина прямоугольника
P=(16+28)*2=88(дм)- периметр прямоугольника
ответ:88дм