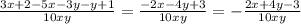Дана трапеция АВСД. Основание АД=22. ДМ - биссектриса, точка М - точка пересечения биссектрисы и боковой стороны АВ, АМ=10, МВ=5
Проведём прямую МК параллельную АД, /КМД=/МДА - накрест лежащие. /КДМ=/МДА, т.к. ДМ - биссектриса, следовательно, /КДМ=/КМД, т.е. треугольник МКД равнобедренный (по признаку), имеем МК=КД, но КД=АМ=10, то МК=10
МН - высота треугольника АМД, в нём АН=(22-10):2=6 (по свойству оснований равнобокой трапеции). По Т.Пифагора находим МН как катет прямоугольного треугольника АМН с гипотенузой 10 и другим катетом 6, МН=8.ВО перпендикуляр к МК. Треугольники АМН и МВО подобны с к=2, т.е. ВО=8:2=4, МО=6:2=3.
Имеем: высота трапеции равна 8+4=12, второе основание ВС=10-3·2=4 (по свойству оснований равнобокой трапеции)
Площадь трапеции равна полусумме оснований умноженная на высоту, т.е. S=(4+22):2·12=156
х кг -половина веса дяди Федора.
2х (кг) - вес дяди Федора.
10 кг - вес Матроскина, по условию задачи.
10+х (кг) - вес Шарика, который больше веса Матроскина на половину веса дяди Федора, из условия задачи.
10+(10+х) (кг) - вес дяди Федора, столько сколько весят Шарик и Матроскин вместе, из условия задачи. Также вес дяди Федора равен 2х (кг)
Тогда:
10+(10+х)=2х
10+10+х=2х
20+х=2х
20=2х-х
х=20 (кг) - половина веса дяди Федора.
20*2=40 (кг) - вес дяди Федора.
10+20=30 (кг) - вес Шарика.
10+30+40=80 (кг) - весят все трое из Простоквашино.
ответ: 80 кг.
а)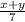
б)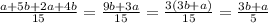
в)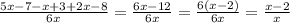
г)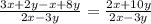
д)