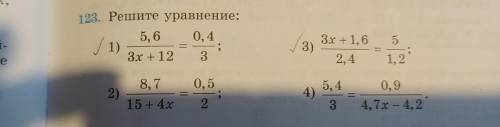
1. Найдем значение выражения:
5/8 * (-3,62) - 1,18 * 5/8 = 5/8 * (-3,62 - 1,18) = 5/8 * (-4,8) = -5/8 * 48/10 = -6/2 = -3.
2. Упростим выражения:
1) 6 + 4а - 5а + а - 7а = 6 - а + а - 7а = 6 - 7а;
2) 5 * (-2) - 6 * (n + 3) - 3 * (2n - 9) = -10 - 6n - 18 - 6n + 27 = -1 - 12n;
3) 5/7 * (2,8c - 4 1/5d) - 2,4 * (5/6c - 1,5d) = 5/7 * 28/10c - 5/7 * 21/5d - 24/10 * 5/6c + 24/10 * 15/10d = 2c - 3d - 2c + 3,6d = 0,6d.
3. Решим уравнение:
0,8 * (x - 2) - 0,7 * (x - 1) = 2,7;
0,8x - 1,6 - 0,7x + 0,7 = 2,7;
0,1x = 2 + 1,6;
x = 3,6 : 0,1;
x = 36.
ответ: х = 36.
Вариант 1:
основное свойство пропорции (6 класс математика)
если a : b = c : d, то a x d = c x b
для нашего случая получим:
5,6 х 3 = 0,4 х (3х + 12)
16,8 = 1,2х + 4,8
1,2х = 16,8 - 4,8
1,2х = 12
х = 12 : 1,2
х = 10
Вариант 2:
5,6 = 0,4 х 14
3х + 12 = 3 х (х + 4)
< var > \frac{0,4}{3} = \frac{0,4 \cdot 14}{3 \cdot (x+4)} < /var ><var>
3
0,4
=
3⋅(x+4)
0,4⋅14
</var>
это возможно только тогда, когда
< var > \frac{14}{(x+4)} = 1 < /var ><var>
(x+4)
14
=1</var>
получается, что числитель и знаменатель равны
14 = х + 4
х = 14 - 4
х = 10