Пошаговое объяснение:
Нам необходимо перемножить две десятичные дроби. Для начала представим их в виде неправильных дробей:
 - в данной дроби 25 целых и 45 сотых. Запишем это в виде дроби с целой частью:
- в данной дроби 25 целых и 45 сотых. Запишем это в виде дроби с целой частью: 
Для удобства, мы можем сократить дробную часть на 5 в числителе и знаменателе: 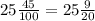
Теперь переведем в неправильную дробь: 
Далее, разберемся с дробью 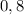 . Запишем ее в виде:
. Запишем ее в виде:  , сократим числитель и знаменатель на 2:
, сократим числитель и знаменатель на 2:  .
.
Теперь запишем произведение двух преобразованных дробей: . Имеем право сократить числитель второй дроби со знаменателем первой, получим:
. Имеем право сократить числитель второй дроби со знаменателем первой, получим:  .
.
Получили неправильную дробь, из которой нужно выделить целую часть. В 509 20 целых частей, так как ближайшее число, которое делится на 25, это 500, а 9 получаем в остатке. Запишем:

Чтобы вернуться обратно в десятичную дробь, необходимо знаменатель домножить на 4, чтобы он стал равен 100, получим:
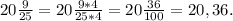
Чтобы разделить дробь на натуральное число, надо знаменатель дроби умножить на число, а числитель оставить тем же. То есть,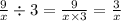 , но для решения задачи оставим дробь в таком виде:
, но для решения задачи оставим дробь в таком виде: 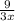 .
.
По условию задачи,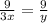 . Между дробями стоит равенство, числители равны, значит и знаменатели равны,
. Между дробями стоит равенство, числители равны, значит и знаменатели равны, 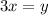 .
.