Пошаговое объяснение:
1) (1+m)²>(m+6)(m-4)
1+2m+m²>m²+6m-4m-24
1+2m+m²>m²+2m-24
1+2m+m²-(m²+2m-24)>0
1+2m+m²-m²-2m+24>0
25>0 это верно!
2) 30mn≤9m²+25n²
9m²+25n²-30mn≥0
(3m)²-2·(3m)·(5n)+(5n)²≥0
(3m-5n)²≥0 это верно!
квадрат любого числа ≥0
1) Область определения функции у = 2 - 1/х:
(-∞; 0) ∪ (0; +∞)
2) Область определения функции у = 2 - 1/(х-2):
(-∞; 2) ∪ (2; +∞)
Пошаговое объяснение:
1) Область определения функции у = 2 - 1/х:
х - любое, кроме х = 0, т.к. на ноль делить нельзя.
ОДЗ: х ≠ 0.
То же, в математических символах:
(-∞; 0) ∪ (0; +∞)
2) Область определения второй функции:
х - любое, кроме х = 2, т.к. в этом случае знаменатель превращается в ноль, а на ноль делить нельзя.
ОДЗ: х ≠ 2.
То же, в математических символах:
(-∞; 2) ∪ (2; +∞)
3) Графики функций по схеме преобразования - в прикреплении:
по п. а) - 3 графика;
по п. б) - 4 графика.
Построение каждого графика сопровождается комментариями: как последовательно из гиперболы были построены графики заданных функций. В прикреплении один и тот же файл дан и в WORD'e, и в PDF, т.к не знаю, какой из них у Вас лучше откроется.
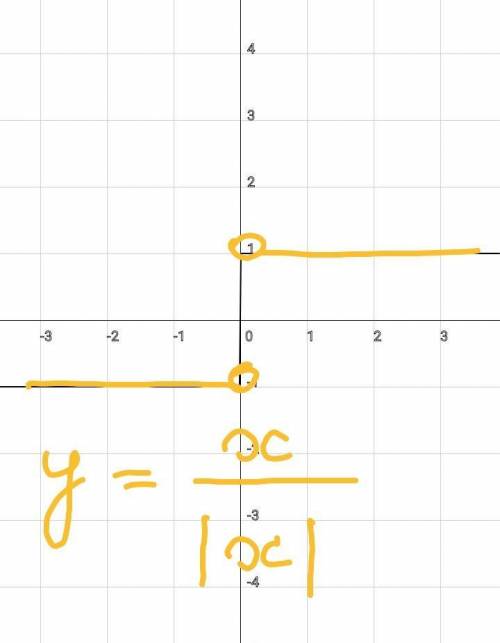
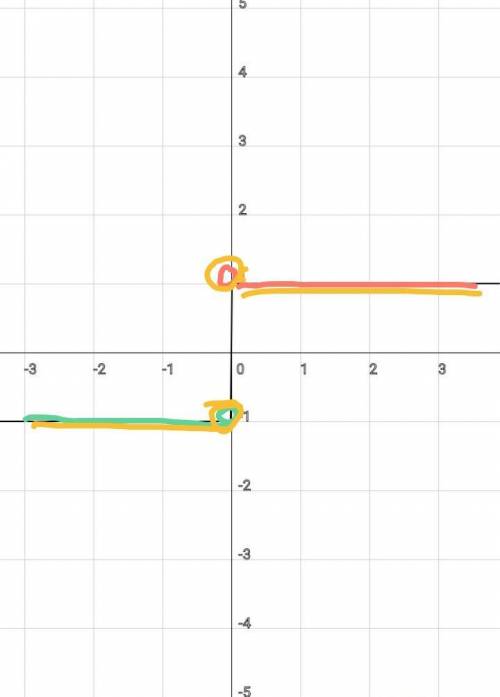
Эти функции не то чтобы пересекаются, они полностью совпадают друг с другом.
Вообще, чтобы понять, пересекаются ли графики функций, нужно приравнять их между собой и найти x, при котором они пересекаются, если такого x не будет, то они не пересекаются.
Но здесь достаточно просто посмотреть на графики этих функций и понять.
Первая функция принимает значения 1 при всех положительных значениях переменной x и значение -1 при всех отрицательных значениях переменной x. В нуле функция не определена.
То же самое происходит и со второй функции.
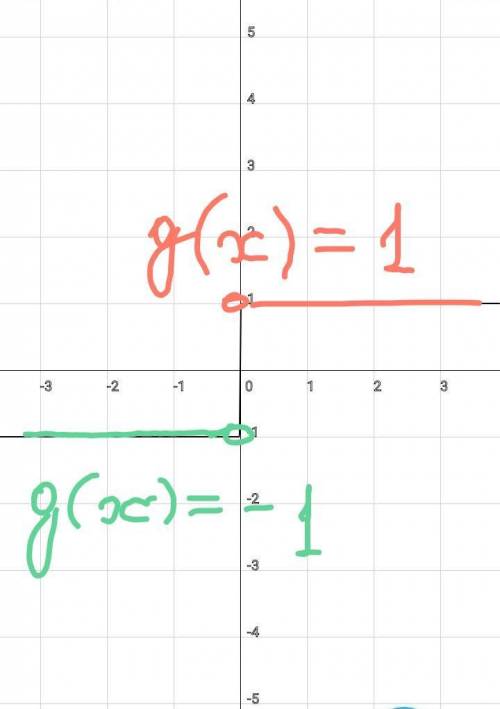
решила первое,второе не смогла.