Пошаговое объяснение:
1)а=2³×3×5 и b=2×3×5²
b=2×3×5×5
а=2×2×2×3×5
НОК(а;b)=2×3×5×5×2×2=600
2)с=2⁴×3²и d=2²×3²×⁵
d=2×2×3×3×5
с=2 × 2 x 2 x 2 x 3 x 3
НОК(с;d)=2 x 2 x 3 x 3 x 5 x 2 x 2 =720
3)е=2³×3×7 и f=2²×3²×7
f=2 x 2 x 3 x 3 x 7
е=2 x 2 x 2 x 3 x 7
НОК(е;f)=2 x 2 x 3 x 3 x 7 x 2=504
4)m=2²×3² и n=3³×5
m= 2 x 2 x 3 x 3 x 3
n=3 x 3 x 3 x 5
НОК(m;n)=2 умножить на 2 x 3 X 3 x 3 x 5
5)р=3×3²×11 и t=2³×3×11
t=2 х 2 х 2 х 3 х 11
р=2 х 3 х 3 х 11
НОК(р;t)=2 х 2 х 2 х 3 х 11 х 3 = 792
6)х=2⁴×3×5 и у=2²×3×5²
у=2 x 2 x 3 x 5 x 5
х=2 x 2 x 2 x 2 x 3 x 5
НОК(х;у)=2 умножить на 2 x2× 3 x 5 x 5 x 2 x 2=1200
объяснение:
разложим числа на простые множители.сначала запишем разложение на множители самого большого числа, затем меньшее число.чтобы определить НОК,необходимо недостающие множители добавить к множителем большего числа и перемножить их
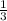часть всех запасов сахара для дрессуры, то у него осталась 
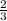запасов сахара для дрессуры, т.е. в 
раза больше, чем он потратил. Поскольку 
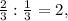или иначе говоря, поскольку 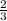вдвое больше, чем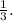 
кусков сахара.
недели.
недель.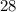
кусков сахара за недели, а значит, в неделю он тратил в два раза меньше, т.е.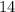 
кусков сахара в неделю.
кусков сахара в неделю.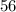
кусков после начальной дрессуры, то при расходе кусков сахара в неделю ему хватит этого остаточного запаса на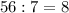 
недель.
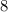недель.
5/6 >5/8,_ 17/30< 2/3,_ 79/68 >5/113,_ 11/12 < 19/20,_ 2³/₁₆ < 2⁹/₁₆
Пошаговое объяснение:
1) При сравнении дробей с одинаковым числителем больше та дробь, знаменатель которой меньше.
5/6> 5/8 ( На чем больше частей делится что-то, тем меньше получится каждая часть).
2) 17/30 и 2/3 приведем к общему знаменателю:
17/30 <20/30 ( при сравнении дробей с равными знаменателями больше та, у которой больше числитель. Если что-то разделить на 30 частей , то 17 частей меньше. чем 20 таких же).
3) 79/68 и 5/113
Первое число - неправильная дробь, оно больше едииницы. Второе - меньше единицы. Поэтому
79/68 > 5/113
4) 11/12 и 19/20
Первому числу до целого недостает 1/12, второму 1/20.
Т.к. 1/12> 1/20, то 19/20>11/12 ( см. объяснение п. 1)
5) Из смешанных чисел с равной целой частью больше та, у которого больше дробная часть. 2=2, 9/16>3/16, поэтому 2 целых и 3/16 меньше, чем 2 целых и 9/16.
хз ;)
Пошаговое объяснение:
я лох,не шарю за математику