
Пошаговое объяснение:
Квадрат гипотенузы равен сумме квадратов катетов
гипотенуза 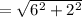 =
= 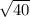
прямоугольные треугольники все равны, значит и гипотенузы их одинаковые. У закрашенной фигуры все стороны равны - это квадрат.
Площадь квадрата равна квадрату длины его стороны.
S =  = 40 см²
= 40 см²
Или второй
можно найти площадь прямоугольных треугольников
S = (6*2) : 2 = 6 см²
Треугольники все одинаковые и их 4
6 * 4 = 24 см² - площадь всех 4 треугольников
Теперь найти площадь большого квадрата
6 + 2 = 8 см - сторона квадрата
8 * 8 = 64 см² - площадь большого квадрата
64 см² - 24 см² = 40 см² - площадь закрашенной фигуры
frac{\pi }{2} +2\pi n,~n\in\mathbb {Z} } , \pi +2\pi k, ~k\in\mathbb {Z} .
Пошаговое объяснение:
\sqrt{1+cosx} =sin x.
1+cosx
=sinx.
Возведем обе части уравнения в квадрат при условии
sinx\geq 0.sinx≥0.
\begin{gathered}1+cosx= sin^{2} x;\\1+cosx=1-cos^{2} x;\\cos^{2} x+cosx=0;\\cosx(cosx+1)=0 ;\\\left [ \begin{array}{lcl} {{cosx=0,} \\ {cosx=-1;}} \end{array} \right.\Leftrightarrow \left [ \begin{array}{lcl} {{x=\frac{\pi }{2} +\pi n,~n\in\mathbb {Z} } \\ {x=\pi +2\pi k, ~k\in\mathbb {Z}}} \end{array} \right.\end{gathered}
Учтем условие , что sinx\geq 0sinx≥0 . Тогда получим
\begin{gathered}\left [ \begin{array}{lcl} {{x=\frac{\pi }{2} +2\pi n,~n\in\mathbb {Z} } \\ {x=\pi +2\pi k, ~k\in\mathbb {Z}}} \end{array} \right.\end{gathered}