Відповідь:
216 треугольников.
Покрокове пояснення:
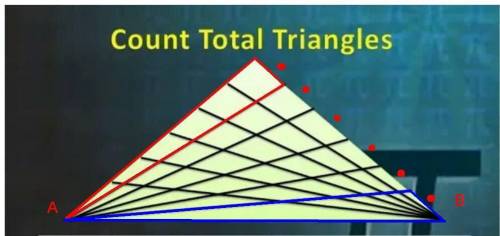
На 1 рисунке в красном треугольнике ( вершина в точке А ) с стороной противолежащей вершине А равной 1 единице находится 6 треугольников, таких треугольников может быть 6 штук ( отмечены точками ). Всего 6 × 6 = 36 треугольников. Аналогичным образом можно построить треугольники с вершиной в точке В. Их будет 6 × 5 = 30 треугольников ( 6 треугольников вошли в 36 с вершиной в точке А ). Итого:
6 × ( 6 + 5 ) треугольников.
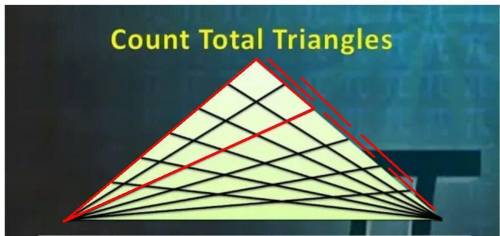
На рисунке 2 проведем аналогичный подсчет числа треугольников:
6 × ( 5 + 4 ) треугольников.
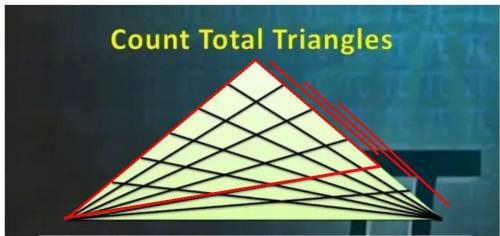
Рисунок 3:
6 × ( 4 + 3 ) треугольников.
Рисунок 4:
6 × ( 3 + 2 ) треугольников.
Рисунок 5:
6 × ( 2 + 1 ) треугольников.
И последний вариант ( сайт не позволяет загрузить больше 5 рисунков ) - 6 треугольников со стороной противолежащей вершине А равной 6 единицам, аналогичные треугольники, построенные с вершиной в точке В - учтены ранее.
Всего:
6 × ( 11 + 9 + 7 + 5 + 3 + 1 ) = 216 треугольников.


(см. объяснение)
Пошаговое объяснение:
В своем ответе я покажу два решения, каждый из которых имеет право на жизнь. Я предпочитаю решать вторым , почему и рекомендую вам начать с него.
Аналитическое решение:
При 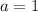 уравнение перестает быть квадратным и принимает линейный вид
уравнение перестает быть квадратным и принимает линейный вид 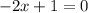 , откуда
, откуда 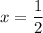 . Значит такое значение параметра нам подходит.
. Значит такое значение параметра нам подходит.
При 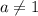 графиком уравнения является парабола.
графиком уравнения является парабола.
Корни будут, если  :
:

Тогда:
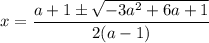 .
.
По условию 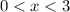 , поэтому:
, поэтому:
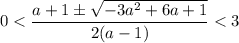
Решив записанную конструкцию выше имеем:
![a\in\left(\dfrac{12}{7};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/5f58c.png) .
.
Итого ответом будет:
![a\in\{1\}\cup\left(\dfrac{12}{7};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/704b1.png)
Достоинства подхода:
Решение "в лоб", особого ума, чтобы понять не надо.Требуются только шаблонные знания математики.Легко написать на компьютере.Недостатки подхода:
Сложные расчеты, повышающие вероятность ошибки.Ограниченность применения.Схематично-графический метод:
Заметим, что при 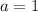 уравнение становится линейным и имеет корень
уравнение становится линейным и имеет корень 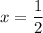 . Тогда такое значение параметра
. Тогда такое значение параметра  необходимо взять в ответ.
необходимо взять в ответ.
Дальнейшее решение выполним, когда 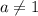 :
:
Введем функцию 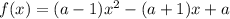 . Тогда
. Тогда 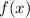 - это парабола.
- это парабола.
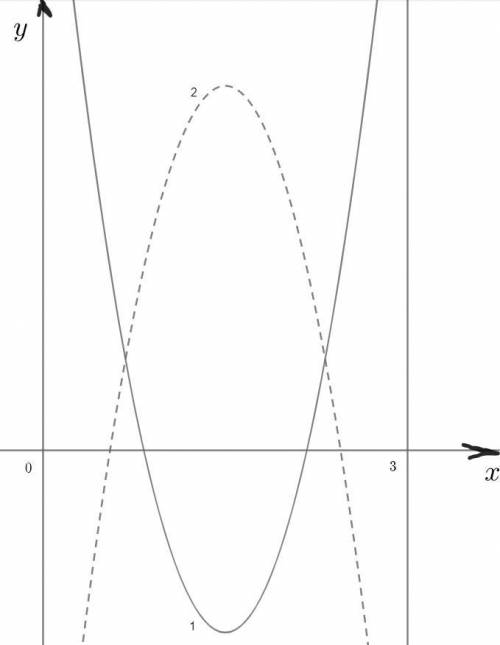
Изобразим эскизы возможного расположения графика 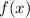 так, чтобы выполнялось условие задачи (я все делаю в единой системе координат, чтоб долго на компьютере не рисовать, вы разбейте на несколько; ситуации пронумерованы и выделены разным типом начертания).
так, чтобы выполнялось условие задачи (я все делаю в единой системе координат, чтоб долго на компьютере не рисовать, вы разбейте на несколько; ситуации пронумерованы и выделены разным типом начертания).
(см. прикрепленный файл)
Опишем эти случаи на языке математики, при условии, что выполняются фразы  и
и 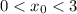 :
:
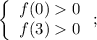 /или/
/или/ 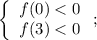
Выполним необходимые расчеты:
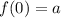
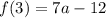
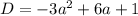
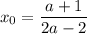
Тогда на условии, что ![a\in\left(\dfrac{4}{5};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/e4b94.png) (посчитано
(посчитано  и
и 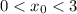 ) системы примут вид:
) системы примут вид:
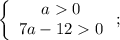 /или/
/или/ 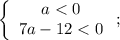
Решить их не составляет труда.
Объединив найденное, получаем, что ![a\in\left(\dfrac{12}{7};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/5f58c.png) .
.
Обратимся к записанному выше и дополним ответ:
![a\in\{1\}\cup\left(\dfrac{12}{7};\;\dfrac{2\sqrt{3}}{3}+1\right]](/tpl/images/2008/6422/704b1.png)
Достоинства подхода:
Наглядное представление решения за счет создания схематичных изображений графиков.Простота вычислений.Понятность, обеспечивающая доступность понимания темы при наличии удовлетворительного уровня подготовки и желания учащегося.Недостатки подхода:
Трудно написать на компьютере.Задание выполнено!
ответ:12 * 7 * 4 = 336