, в одном куске 5 м ткани, в другом куске 7 м такой же ткани. За оба куска заплатил d р. За оба куска заплатили k р. Объясни, что обозначают выражения. k : (5 + 7) k : (5 + 7) • 5 k : (5 + 7) • 7

👇

Увидеть ответ

Ответ:

nastyonakononenkova

06.08.2020

\frac{3}{7}73 ÷ k = 5 ÷ 2\frac{1}{3}231

\frac{3}{7}73 ÷ k = 5 × \frac{3}{7}73

k = \frac{3}{7}73 ÷ \frac{15}{7}715

k = \frac{3*7}{7*15}7∗153∗7

k = \frac{1}{5}51

k = 0,2

2) 5,5 ÷ 8 = k ÷ \frac{2}{11}112

\frac{11}{2}211 × \frac{1}{8}81 = k ÷ \frac{2}{11}112

k = \frac{11*2}{16*11}16∗1111∗2

k = \frac{1}{8}81

k = 0,125

3) k ÷ \frac{5}{9}95 = 1\frac{4}{5}154 ÷ 6

k ÷ \frac{5}{9}95 = \frac{9}{5*6}5∗69

k = \frac{5*3}{9*10}9∗105∗3

k = \frac{1}{6}61

4) 20 ÷ 3\frac{1}{4}341 = \frac{4}{13}134 ÷ k

\frac{20*4}{13}1320∗4 = \frac{4}{13}134 ÷ k

k = \frac{4*13}{13*80}13∗804∗13

k = \frac{1}{20}201

k = 0,05

4,4(24 оценок)

Открыть все ответы

Ответ:

inna0509781

06.08.2020

По теореме о пропорциональных отрезках,

\displaystyle \frac{BE}{EA}=\frac{BF}{FC}

Раз BF относится к FC как 5 : 3 (по условию), то так же относится и BE к EA.

Пусть коэффициент пропорциональности равен x, тогда BE = 5x, EA = 3x.

BE + EA = AB = 64, поэтому можем составить такое уравнение:

5x + 3x = 64

8x = 64

x = 64 : 8

x = 8

BE = 5 · 8 = 40 (см).

Дано:

АЕ = 18 см;

ВC : BF = 3 : 2

Найти: АВ.

По теореме о пропорциональных отрезках,

\displaystyle \frac{BA}{BE}=\frac{BC}{BF}

Раз BC относится к BF как 3 : 2 (по условию), то так же относится и BA к BE.

Пусть коэффициент пропорциональности равен x, тогда BA = 3x, BE = 2x.

BA = BE + EA.

3х = 2х + 18

3х - 2х = 18

х = 18

BA = 3 · 18 = 54 (cм).

Дано:

BE = 12 см;

AE : FC = 4 : 5

Найти: BF.

По теореме о пропорциональных отрезках,

\displaystyle \frac{BE}{BF}=\frac{EA}{FC}

\displaystyle \frac{12}{BF}=\frac{4}{5}

Для того чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов разделить на известный средний:

\displaystyle BF = \frac{12\cdot 5}{4}= 15BF=

12⋅5

=15 (см).

ответ: а) 40 см; b) 54 см; c) 15 см.

4,5(36 оценок)

Ответ:

gameralphac

06.08.2020

20 грамм соли содержал раствор.

Пошаговое объяснение:

Требуется найти, сколько грамм соли содержал раствор?.

Пусть в первоначальном растоворе - х г соли, воды - 60 г.

Тогда масса всего раствора (60 + х) г.

Чтобы узнать сколько процентов первое число от второго, надо первое число разделить на второе, а результат умножить на 100.

Найдем процентное содержание соли в первом растворе:

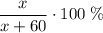
$\displaystyle \frac{x}{x+60} \cdot100\;\%$

Во втором растворе соли осталось столько же, то есть х г.

Воды стало (60 + 20) = 80 (г).

Тогда процентное содержание соли:

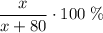
$\displaystyle \frac{x}{x+80} \cdot100\;\%$

Знаем, что разница процентного содержания соли в двух растворах составляет 5%.

Составим и решим уравнение:

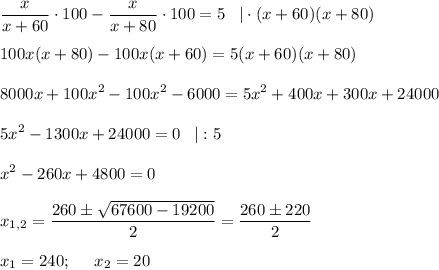
$\displaystyle \frac{x}{x+60} \cdot100-\displaystyle \frac{x}{x+80} \cdot100=5\;\;\;|\cdot(x+60)(x+80)100x(x+80)-100x(x+60)=5(x+60)(x+80)8000x+100x^2-100x^2-6000=5x^2+400x+300x+240005x^2-1300x+24000=0\;\;\;|:5x^2-260x+4800=0x_{1,2}=\frac{260\pm\sqrt{67600-19200} }{2}=\frac{260\pm220}{2}\\ \\ x_1=240;\;\;\;\;\;x_2=20$