0,99144
Пошаговое объяснение:
Для решения задачи воспользуемся формулой Бернулли для повторных испытаний. Пусть вероятность изделия оказаться бракованным это p=0,1. Вероятность изделия оказаться хорошим это q=0,9.
Партия будет принята без сплошного контроля, если из пяти изделий не будет вообще бракованных, либо одно бракованное, либо - два.
Найдем по очереди вероятности каждого из подходящих исходов:
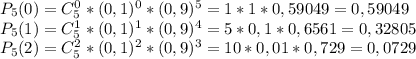
Просуммируем полученные вероятности:
0,59049+0,32805+0,0729=0,99144
Это и будет вероятность того, что партия будет принята без сплошного контроля.
Нехай Похила перетинає площину в точці B.
З точки а опустимо перпендикуляр до площини α в точку С, що належить площині. АС і буде відстанню від точки А до площини. ВС - проекція похилої.
У прямокутному трикутнику АВС відома гіпотенуза АВ, рівна 6 см, і кут в = 60 градусів. Знайдемо катети.
Кут в дорівнює 60 градусам, тоді кут А дорівнює 30.
Катет, що лежить проти кута А дорівнює половині гіпотенузи, значить
НД = 1/2*АВ = 1/2 * 6 = 3 см.
За теормеме Піфагора знаходимо другий катет
АС = √(АВ2-ВС2) = √(36-9) = √25 = 5,
Відповідь: 3 см - Довжина проекції, 5 см - відстань від точки А до площини.
Дано: A(14;3); B(26;7); C(22;19); D(10;15).
Решение.
1) Найдём стороны четырёхугольника ABCD.
Стороны четырёхугольника ABCD равны между собой.
2) Найдём диагонали четырёхугольника ABCD.
Диагонали четырёхугольника ABCD равны между собой.
3) Если стороны четырёхугольника ABCD равны между собой и его диагонали равны между собой, значит, четырёхугольник ABCD - квадрат.
Доказано.
4) Найдём - площадь квадрата ABCD.
- площадь квадрата ABCD.
ответ: