Поскольку Маша не может выговорить буквы М и Ш, она не сумеет произнести числа, содержащие в себе цифры 7 (сеМь), 8 (восеМь), и 6 (Шесть).
То есть, чтобы понять, сколько чисел от 1 до 1000 она сможет правильно произнести, нужно понять, сколько однозначных, двузначных и трехзначных чисел не содержат в своей записи цифры 6, 8 и 7.
1) Найдем, сколько таких однозначных чисел.
Раз цифр всего 10, и мы исключаем 0 (числа идут от 1), 6, 8 и 7, то есть 4 цифры, остается 6 вариантов.
2) Найдем, сколько двузначных чисел, в которых не содержится ни 6, ни 7, ни 8.
Первая цифра не может быть ни 0 (число не может начинаться с нуля), ни 6, ни 7, ни 8, — значит, 6 вариантов первой цифры.
Вторая цифра не может быть ни 6, ни 7, ни 8, — значит, 7 вариантов второй цифры.
Согласно комбинаторному правилу умножения, если объект А можно выбрать n количеством , а объект B — m количеством , то пару объектов можно выбрать .
Таким образом, вариантов двузначных чисел, не содержащих 6, 7 и 8, всего 42.
3) Рассмотрим трехзначные числа.
Первая цифра в них не может быть 0, 6, 7 или 8, — остается 6 вариантов.
Вторая цифра не может быть 6, 7, 8, — 7 вариантов.
Аналогично, существует 7 вариантов третьей цифры.
Получаем =294 варианта подходящих нам трехзначных чисел.
Суммируем варианты однозначных, двузначных и трезначных чисел от 1 до 1000, не содержащих цифр 6, 7 и 8:
Гармонические ступени в мажоре 6пониженная, в миноре 7повышенная Уменьшенный септ стоит на 7(или 7 повышенная в миноре, в мажоре просто 7). Его обращения квинтсекст на 2, терцкварт на 4; секунд на 6( или 6пониженной в мажоре, в миноре просто 6) Двойная доминанта всегда с повышеным VIст.
In userer Schule tragen die Schüler keine Schuluniform.Die Mädchen tragen gewöhnlich Röcke,Blusen,Hosen,T-Shirts,Kleider und Blazer.Die Jungen tragen Hemden und Hosen,T-Shirts und manchmal Anzüge.Die Schüler unserer Schule sollen auch nicht die Schuluniform tragen. Ich trage natürlich auch keine Schuluniform.Ich würde sie auch nicht gern tragen.Dann bist du jeden Tag gleich und siehst wie alle anderen Schüler aus.Dabei verlierst du deine Individualität und bist nicht mehr für deine Umgebung interessant.Ich bin eindeutig gegen die Schuluniform.Ich finde die Schuluniform veraltet und alltäglich.
Поскольку Маша не может выговорить буквы М и Ш, она не сумеет произнести числа, содержащие в себе цифры 7 (сеМь), 8 (восеМь), и 6 (Шесть).
То есть, чтобы понять, сколько чисел от 1 до 1000 она сможет правильно произнести, нужно понять, сколько однозначных, двузначных и трехзначных чисел не содержат в своей записи цифры 6, 8 и 7.
1) Найдем, сколько таких однозначных чисел.
Раз цифр всего 10, и мы исключаем 0 (числа идут от 1), 6, 8 и 7, то есть 4 цифры, остается 6 вариантов.
2) Найдем, сколько двузначных чисел, в которых не содержится ни 6, ни 7, ни 8.
Первая цифра не может быть ни 0 (число не может начинаться с нуля), ни 6, ни 7, ни 8, — значит, 6 вариантов первой цифры.
Вторая цифра не может быть ни 6, ни 7, ни 8, — значит, 7 вариантов второй цифры.
Согласно комбинаторному правилу умножения, если объект А можно выбрать n количеством , а объект B — m количеством , то пару объектов можно выбрать .
Таким образом, вариантов двузначных чисел, не содержащих 6, 7 и 8, всего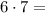
42.
3) Рассмотрим трехзначные числа.
Первая цифра в них не может быть 0, 6, 7 или 8, — остается 6 вариантов.
Вторая цифра не может быть 6, 7, 8, — 7 вариантов.
Аналогично, существует 7 вариантов третьей цифры.
Получаем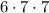
=294 варианта подходящих нам трехзначных чисел.
Суммируем варианты однозначных, двузначных и трезначных чисел от 1 до 1000, не содержащих цифр 6, 7 и 8:
ответ: 342.