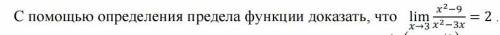
кароче 1:4- это отношение,то есть сокращение дробей.И вот если надо найти изначально число и нам дано сколько выйдет если (числитель с знаменатилям)то можно решить уравнение,например есть число 1:4 и если соединить дроби (изначально дробь без сокращении)то будет 20,решение:1×+4×=20, 5×=20 ×=4 и потом надо умножть.
Проценты:чтоб найти проценты надо решать пропорцией.И писать проценты внизу процент а цифры внизу цифр.Например:
120 это 100%,найдите 20%
120-100%
×-20%(× берем как за неизвестность)
и здесь умножаем бабочкай:20×120:100=24
Точно так же назодить цифры от цисел
кароче 1:4- это отношение,то есть сокращение дробей.И вот если надо найти изначально число и нам дано сколько выйдет если (числитель с знаменатилям)то можно решить уравнение,например есть число 1:4 и если соединить дроби (изначально дробь без сокращении)то будет 20,решение:1×+4×=20, 5×=20 ×=4 и потом надо умножть.
Проценты:чтоб найти проценты надо решать пропорцией.И писать проценты внизу процент а цифры внизу цифр.Например:
120 это 100%,найдите 20%
120-100%
×-20%(× берем как за неизвестность)
и здесь умножаем бабочкай:20×120:100=24
Точно так же назодить цифры от цисел
Пошаговое объяснение:
Пусть ε - сколь угодно малое положительное число. Мы докажем утверждение, если найдём такое число δ>0, если для всех x∈(3-δ; 3+δ) будет выполняться неравенство /(x²-9)/(x²+3*x)-2/<ε. Это неравенство равносильно двойному неравенству 2-ε<(x²-9)/(x²+3*x)<2+ε. Их общим решением является x∈(3/[1+ε];3)∪(3;3/[1-ε]). Так как число 3/(1+ε) "ближе" к 3, чем число 3/(1-ε), то возьмём δ=3-3/(1+ε)=3*ε/(1+ε). Таким образом, число δ найдено, а это и доказывает справедливость равенства.