Пошаговое объяснение:
Такие задачи решаются с уравнений.
Так составим же его.
Обозначим за x количество яблок, собранных Ирой. (Про кол-во собранных Ирой яблок информации мало, поэтому именно ее за икс обозначим).
Тогда Вера собрала 3x яблок(т.к. в 3 раза больше собрала, чем Ира).
А Настя - x - 8(т.к. собрала на 8 яблок меньше).
Так как у нас есть общее кол-во яблок(62), то и наше уравнение в сумме будет составлять 62.
Получим:
3x + x + x - 8 = 62
Сложим между собой иксы, а -8 перенесем вправо с изменением знака на противоположный.
Получим:
5x = 62 + 8
5x = 70 |:5
x = 14 - собрала Ирина.
Найдем, сколько яблок собрала Вера: 14 * 3 = 42 яблока.
А теперь вычислим, сколько яблок собрала Настя: 14 - 8 = 6 яблок.
Задача решена.
84
Пошаговое объяснение:
Треугольник является прямоугольным, значит, у него два катета a и b, гипотенуза c. По условию одна из сторон 12 (единицу можно выбрать произвольное). Эта сторона будет катетом, в противном случае, если эта сторона гипотенуза c, то из-за ограничения для катетов a<c и b<c максимально возможный периметр также ограничивается. Поэтому наименьший катет, пусть этот катет будет a, выберем как a=12.
Так как треугольник прямоугольный, то верна теорема Пифагора
c² = a² + b² или c² - b²= 12² или (c - b)·(c + b)= 144.
С другой стороны, из условия существования треугольника (другое название - неравенство треугольника) получаем
a + c > b
b + c > a
a + b > c
Из последнего неравенства вытекает, что 12 > c - b.
Теперь рассмотрим (c - b)·(c + b)= 144. Из того, что длины сторон треугольника являются целыми числами (вообще то натуральными числами), то (c - b) и (c + b) также являются натуральными числами.
Обозначим c - b = х. Отсюда c = x + b. Тогда
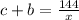
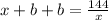
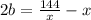
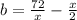
Отсюда следует, что х - чётное и является делителем 72.
Учитывая 12 > c - b и то, что чем меньше c - b, тем больше периметр, рассмотрим разложение числа 144 на чётные множители: 144=2·72.
Тогда c - b = 2 и c + b = 72. Отсюда c = 37 и b = 35. Ясно, что неравенство треугольника выполняется, оба числа целые.
Проверим утверждение теоремы Пифагора:
12²+35²=144+1225=1369=37².
Значит, все условия выполняются. Тогда максимально возможный периметр равен сумме длин сторон треугольника
P = a + b + c = 12 + 35 + 37 = 84
Пошаговое объяснение:
Используем удобное вычисление:
а) 6,89 + 5,37 + 3,11 + 7,63=(6,89 +3,11) + (5,37 +7,63)= 10+13=23;
б) 4 5/13 + 8 7/15 + 11 8/13 + 14 8/13=(4 5/13 + 11 8/13 + 14 8/13)+( 8 7/15 )=
=(4+11+14) (5+8+14)/13 + 8 7/15 = 29 27/13 + 8 7/15=31 1/13 + 8 7/15 =
=>НОК(13;15)=195=> 31 15/195 + 8 91/195 = 39 106/195.