Пошаговое объяснение:
Пусть скорость Бомбура = х, тогда скорость Фили = 3х, а скорость Кили = 6х.
Каждый из них пробежал по одной трети всего пути, то есть если весь путь = S, то расстояние, которое пробежал каждый гном = S/3.
Время, которое бежал Бомбур = S/3 ÷ x = S/3 · 1/x
Время, которое бежал Фили = S/3 ÷ 3x = S/3 · 1/3x
Время, которое бежал Кили = S/3 ÷ 6x = S/3 · 1/6x
Общее время, которое бежали три гнома эстафетой = S/3 · (1/x + 1/3x + 1/6x) = S/3 · (6/6x + 2/6x + 1/6x) = S/3 · 9/6x = S/3 · 3/2x = S/2x
Теперь у нас есть все необходимые данные для вычисления скорости Торина. Время , которое он бежал = S/2x . Расстояние, которое он преодолел = S.
Итак, по формуле v = S/t :
Скорость Торина = S ÷ S/2x = S · 2x/S = 2x
Как нетрудно догадаться, скорость Торина 2х в два раза больше чем скорость Бомбура х.
ответ: в 2 раза.
Відповідь:
1 та 2
Пояснення:
Розкладемо ліву частину нерівності на множники, розв'язавши відповідне квадратне рівняння:
-2x²+5x-2 = 0
2x²-5x+2 = 0
D = b²-4ac = (-5)²-4·2·2 = 25-16 = 9
x_1 = (-b+√D)/2a = (5+√9)/(2·2) = (5+3)/4 = 2
x_2 = (-b-√D)/2a = (5-√9)/(2·2) = (5-3)/4 = 0,5
Тоді -(2x²-5x+2) = -2(x-0,5)(x-2) = (2x-1)(2-x)
Тепер нерівність перетворена до такої: (2x-1)(2-x) ≥ 0
Розв'яжемо її методом інтервалів. Позначимо нулі функції в лівій частині нерівності (корені щойно розв'язаного рівняння) на числовій прямій та з'ясуємо знак цієї функції на кожному з проміжків, які утворяться (проставимо "+" або "-").
- + -
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0,5)¯¯¯¯¯¯¯¯¯¯¯¯¯¯(2)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Множиною розв'язків буде проміжок, на якому функція набуває невід'ємних значень. Тобто x ∈ [0,5; 2]. Йому належать лише два цілих числа: 1 та 2.
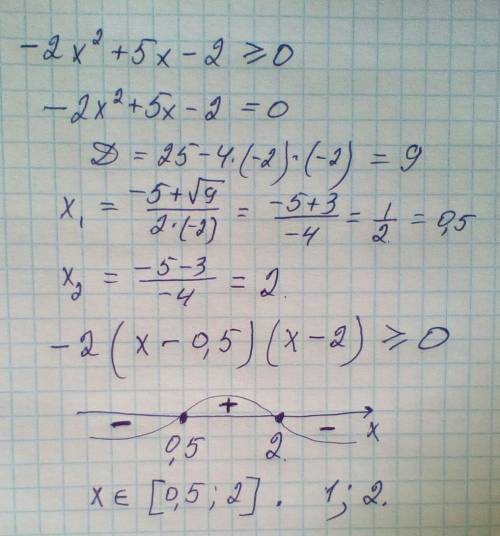
Пошаговое объяснение:
а)15/46=270/828 и 17/36=391/828
б) 11/34=33/102 и 12/51=24/102
в) 1/2=17/34 3/17=6/34 и 5/34=5/34