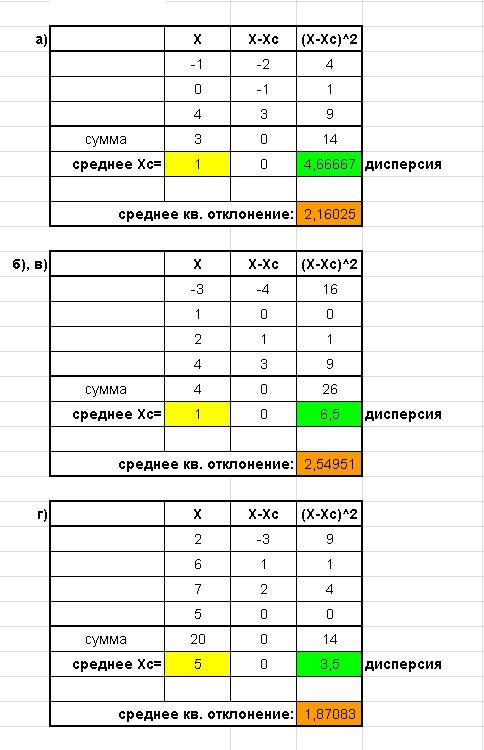
Картинка с табличками вложена. Искомые величины выделены цветом.
а)
Сначала находим среднее значение выборки:
Хс = (-1 + 0 + 4)/3 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n}} = \\
\sqrt{\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 2,1602
Дисперсия - это средний квадрате отклонений от средней величины:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2}{n} = \\
\frac{(-1 - 1)^2 +(0 - 1)^2 +(4 - 1)^2}{3}} = 4,6667
б)
Среднее значение выборки:
Хс = (-3 + 1 + 2 + 4)/4 = 1
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 2,5495
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} = \\
\frac{(-3 - 1)^2 +(1 - 1)^2 +(2 - 1)^2 + (4 - 1)^2}{4}} = 6,5
в) смотри б)
г)
Среднее значение выборки:
Хс = (2 + 6 + 7 + 5)/4 = 5
Среднее квадратичное отклонение:
\sqrt{\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n}} = \\
\sqrt{\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 1,8708
Дисперсия:
\frac{(X1 - Xc)^2 +(X2 - Xc)^2 +(X3 - Xc)^2+(X4 - Xc)^2}{n} =
\frac{(2 - 5)^2 +(6 - 5)^2 +(7 - 5)^2 + (5 - 5)^2}{4}} = 3,5
а) Екі ауылдан бір мезгілде бір−біріне қарама−қарсы шыққан екі салт атты 3 сағаттан кейін кездесті. 1−жылд.12км/сағ, 2−жылд. 15км/сағ. Екі ауылдың арақашықтығын тап.
12км/сағ 3 сағ 15км/сағ
(12+15)×3=81 (км) – қашықтық
Ж:
ә) Арақашықтығы 81км кеі ауылдан бір мезгілде екі салт атты бір−біріне қарама−қарсы шығып, 3 сағаттан кейін кездесті. 1−жылд. 12км=сағ. 2−жылдамдықты тап.
12км/сағ 3 сағ ?км/сағ
81 км
81:3–12=15 (км/сағ) – екінші жылдамдық
Ж:
Б) Арақашықтығы 81км екі ауылдан бір мезгілде екі салт атты бір−біріне қарама−қарсы шықты. 1−жылд. 12км/сағ, ал екінші жылд. 15кмсағ. Олар неше сағаттан кейін кездесті?
81: (12+15)=3 (сағ)
в любом случае 1
это во всех правилах прописано