
Если конфеты в наборе не будут повторяться
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
Чтобы наборы отличались, только 6 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки без повторений :

ответ : 6 детей
=====================================
Если конфеты в наборах могут повторяться, добавится ещё 4 варианта
Дети могут взять по две конфеты :
1) кс, ск - карамель, суфле
2) ки, ик - карамель, ирис
3) кт, тк - карамель, трюфели
4) си, ис - суфле, ирис
5) ст, тс - суфле, трюфели
6) ит, ти - ирис, трюфели
7) кк - карамель, карамель
8) сс - суфле, суфле
9) ии - ирис, ирис
10) тт - трюфели, трюфели
10 детей могут взять по 2 конфеты.
Решение по формуле сочетаний из 4 типов конфет по 2 штуки с повторениями :
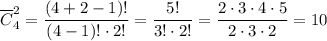
ответ : 10 детей
4m^2+25n^2-20mn=(2m-5n)^2
12xy+9x^2+4y^2=(2e+5x)^2
m^2+n^2p^2-2mnp=(m-np)^2
a^2c^2+2abc+b^2=(ac+b)^2
2xyz+x^2z^2+y^2=(y+xz)^2
здесь ^2- возведение в квадрат