28,8 т зерна.
Пошаговое объяснение:
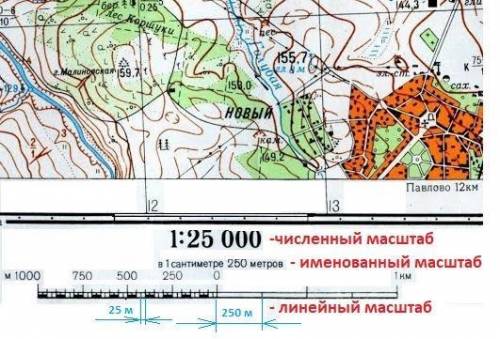
Разные виды масштаба приведены на рисунке в приложении.
Нам задан численный масштаб - М 1 : 10 000.
Переведем его в именованный масштаб и получим:
В 1 см - 10 000 см = 100 м или словами: В 1 см 100 м или k = 100 м/см
Находим реальные размеры участка - умножением на k.
a = 12 см * 100 м/см = 1200 м - длина
b = 10 см *100 м/см = 1000 м - ширина
Находим площадь участка: 1 га = 100*100 = 10 000 м²
S = a*b = 1200 *1000 = 1 200 000 м² = 120 га - площадь.
Находим расход зерна - умножением.
M = 0.24 т/га * 120 га = 28,8 т зерна - ответ.
Из условия задачи, имеем
b1+b1q=108 => b1(1+q)=108
b1q+b1q^2=135 => b1(q+q^2)=135
из первого уравнения получаем
b1=108/(1+q) , q не равно -1
Подставим во второе уравнение
(108/(1+q))*(q+q^2)=135
108(q+q^2)=135(1+g)
108q^2+108q-135q-135=0
108q^2-27q-135=0
4q^2-g-5=0
Решая это квадратное уравнение, получаем корни
q=-1 - не удовлетворяет ОДЗ
q=1,25
тогда b1=108/(1+q)=108/2,25=48
1 член прогрессии = b1=48
2- = b1q=48*1,25=60
3- =b1q^2=48*(1.25)^2=75