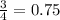Question

Опыт состоит в двукратном подбрасывании игральной кости. Найти вероятность того, что произведение выпавших очков будет четным.

Answer 1

$\frac{3}{4}=0.75$

Пошаговое объяснение:

В принципе, решение можно осуществить 2 путями. Для начала, обозначим вероятности

Pн - нечетное произведение очков,

Рч - четное произведение очков

1. При двух бросках в результате могут быть только 2 вероятных события:

- четное произведение очков

- нечетное произведение очков.

Эти 2 случая охватывают полностью возможные наступления событий.

Соответственно, верно равенство

$P_{ч} + P_{н}=1 \: \: = \: \: P_{ч}=1 - P_{н}$

Произведение 2 чисел будет НЕчетным тогда, когда НЕчетными являются ОДНОВРЕМЕННО ОБА из множителей.

Два броска являются независимыми (результат 2 броска не зависит от числа, выпавшего первым);

Из равновероятных 6 событий для одного броска нечетныеэми будут 3.

Следовательно, вероятность нечетного броска равна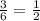 $\frac{3}{6}=\frac{1}{2}$

Вероятность того, что произведение чисел бросков будет нечетным равна вероятности двойного нечетного броска - т.е. произведению вероятностей для 1 и 2 броска:

$P_{н}=P_{1н} \times P_{2н}\: \: \\ P_{н}= \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \\$

Следовательно, вероятность того, что произведение чисел бросков будет четным равна разности между 1 и Рн:

$= \: P_{ч}=1 - P_{н} \\ P_{ч}= 1 - \frac{1}{4} = \frac{3}{4}$

2. Возможны варианты бросков (первый-второй броски):

1 - чч - четный-четный

2 - чн - четный-нечетный

3 - нч - нечетный-четный

4 - нн - нечетный-нечетный.

Произведение же четно, когда четным является ХОТЯ БЫ ОДИН из множителей.

А это происходит в трех случаях из 4-х - случае 1, 2 и 3 из указанных выше.

То есть

$P_{ч}=P_{чн} + P_{нч} + P_{чч}$

Легко проверить, что вероятность наступления каждого из событий равна:

произведению вероятности четности/нечетности первого броска на вероятность четности/нечетности второго броска.

Для любого броска вероятность четного числа очков равна вероятности нечетного и составляет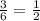 $\frac{3}{6}=\frac{1}{2}$

Следовательно:

$P_{чч}{=}P_{чн}{=}P_{нч}{=} P_{нн}=\frac{1}{2} \times \frac{1}{2} = \frac{1}{4} \\$

А значит,

$P_{ч}=P_{чн} + P_{нч} + P_{чч} = \\ = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4}$

Итак, в двух различных решениях получили одинаковые результаты. Следовательно, ответ верен:

ответ : $\frac{3}{4}=0.75$