Question

Поезд был задержан у семафора на 8 минут и ликвидировал опоздание на перегоне в 40 км, увеличив скорость на 15 км/ч. чему равна скорость поезда по расписанию.

Answer 1

8 мин.=8/60 ч.=2/15 ч.

Пусть х км/ч - скорость поезда по расписанию, тогда увеличенная скорость равна (х+15) км/ч. Поезд проехал перегон в 40 км быстрее, чем обычно, на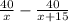 $\frac{40}{x}-\frac{40}{x+15}$ или на $\frac{2}{15}$ часа. Составим и решим уравнение:

$\frac{40}{x}-\frac{40}{x+15}=\frac{2}{15}$    |*$\frac{15}{2}x(x+15)$

$300x+4500-300x=x^2+15x$

$x^2+15x-4500=0$

по теореме Виета:

$x_1=60$  $x_2=-75<0$ (не подходит)

ответ: скорость поезда на этом перегоне по расписанию 60 км/ч.