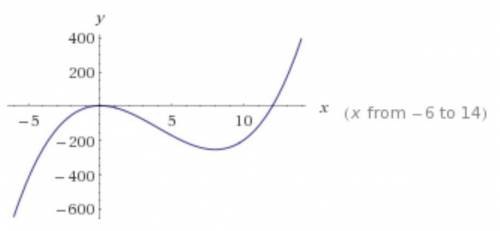
Вид функции на фото.
Для всего остального есть производная. Возьмем ее по х:
y'(x) = 3x^2-24x
Исследуем производную. Для этого приравняем ее к нулю.
3x^2-24x = 0
x = 0 или 3x - 24 = 0
x = 8
подставим эти значения в функцию
x = 0 => y(0) = 4
x = 8 => y(8) = -252
значит, в точках (0,4) и (8, -252) функция имеет экстремумы. => не монотонна.
Посмотрим на вторую производную.
y''(x) = 6x- 24
y''(0) = -24. Если вторая производная в точке отрицательна, то в этом месте функция выпукла вверх.
y''(8) = 24. Если вторая производная в точке положительна, то в этой точке функция выпукла вниз.
можно " лучший ответ" плез)