Question

ДАЮ 40 ! Точка D середина стороны АС треугольника АВС. DE u DF-биссектрисы Треугольников ABD u CBD. Отрезки ВDи EF пересекаются в точке М. докажите, что DM=1/2 EF

Answer 1

Пошаговое объяснение:

Дано: ΔАВС.

AD = DC;

DE u DF-биссектрисы.

Доказать: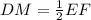 $DM = \frac{1}{2}EF$

Доказательство:

1. Рассмотрим ΔDEF.

∠1 + ∠2 +∠3 +∠4 = 180° (∠ADC - развернутый)

∠1 = ∠2; ∠3 = ∠4 (DE u DF-биссектрисы)

⇒ ∠2 + ∠3 = 90°

⇒ ΔDEF - прямоугольный.

2. Рассмотрим ΔABD.

DE - биссектриса.

Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон .

$\displaystyle \Rightarrow \frac{AE}{AD}=\frac{EB}{BD} \;\;\;$   или   $\displaystyle \frac{EB}{AE}=\frac{BD}{AD}\;\;\;(1)$

3. Рассмотрим   ΔDBC.

DF - биссектриса.

$\displaystyle \Rightarrow \frac{FC}{CD}=\frac{FB}{BD}\;\;\;$   или   $\displaystyle \frac{FB}{FC}=\frac{BD}{CD}\;\;\;(2)$  

4. AD = CD (по условию)

В равенствах (1) и (2) правые части равны, ⇒ равны и левые, то есть:

$\displaystyle \frac{EB}{AE}=\frac{FB}{FC}$

Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные.

⇒ EF || AC

5. Рассмотрим ΔEBM и ΔABD.

EM || AD

Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒ ΔEBM ~ ΔABD , тогда

$\displaystyle \frac{BM}{BD}=\frac{EM}{AD}\;\;\;(3)$

6. Рассмотрим ΔMBF и ΔDBC.

MF || DC

⇒ ΔMBF ~ ΔDBC.

$\displaystyle \frac{BM}{BD}=\frac{MF}{DC} \;\;\;(4)$

В равенствах (3) и (4) левые части равны, ⇒ равны и правые:

$\displaystyle \frac{EM}{AD}=\frac{MF}{DC}$

Так как AD = DC ⇒ EM = MF.

7. Рассмотрим ΔEFD - прямоугольный.

EM = MF ⇒ DM - медиана.

Медиана, проведенная из вершины прямого угла к гипотенузе равна ее половине.

$\displaystyle \Rightarrow DM=\frac{1}{2}EF$