Симметричные и несимметричные плоские фигуры. Определи несимметричные фигуры относительно прямой.
Верных ответов: 2

👇

Увидеть ответ

Ответ:

kamikot

11.12.2021

Пошаговое объяснение:

вторая фигура не симметрична

4,4(78 оценок)

Ответ:

Vakluver

11.12.2021

1 симметричное

Пошаговое объяснения не уверен что будут правильно е:

4,4(21 оценок)

Открыть все ответы

Ответ:

NotLikeThis

11.12.2021

Всего n сторон, на каждой стороне может быть либо +1 либо -1 ( как результат произведения того, что в вершинах: (-1)*(-1) = 1, или (-1)*1 = -1, или 1*1 = 1). Все стороны можно разбить на две группы: те, на которых 1; и те, на которых (-1). Пусть количество сторон первой группы = A, а количество сторон второй группы B.
A>=0; B>=0.
По условию S = A*1 + B*(-1) = A-B = 0. Отсюда следует, что A=B. То есть количество сторон первой группы равно количеству сторон второй группы. Но A+B = n. Отсюда следует, что n = A+A=B+B = 2A=2B.
То есть количество сторон n - это четное число (то есть делится на 2).
Рассмотрим теперь сумму значений в вершинах, пусть для определенности сумма значений в вершинах = m. У нас есть две группы сторон. Каждой стороне можно приписать сумму двух вершин, которые эта сторона соединяет, пусть это будет значение S_i

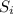, i - это номер стороны (их всего n, их можно занумеровать).
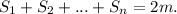Тогда сумма: S_1+ S_2+...+S_n = 2m.

. Почему 2m? Потому что в такой сумме значение в каждой вершине будет подсчитано ДВА РАЗА, так как из каждой вершины выходят две стороны.
Для тех сторон, на которых написано (-1) очевидно S_j

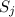будет равно 0. Теперь рассмотрим стороны, на которых написано (1). Их можно также разбить на две группы: те, что соединяют (-1) и (-1), и те, что соединяют (1) с (1). Пусть первых С, а вторых D. Тогда
2m = (-2)*C + (2)*D. Кроме того, C+D=A = n/2. Имеем:
m = D - C;
(n/2) = D+C.
Отсюда (n/2) + m = 2D, или n/2 = 2D - m. Запомним это.
Теперь разобьем сами вершины на две группы - те в которых (-1) - пусть их количество K; и те, в которых (1) - пусть их количество L. Тогда
K+L = n, и m = 1*L + (-1)*K, то есть
L-K = m.
Отсюда n+m = 2L,
и m = 2L - n, т.к. мы доказали ранее, что n - четное, то m - тоже четное, как разность четных чисел (разность четных чисел - всегда четное).
Пусть m = 2*q. Теперь вспомним то равенство: n/2 = 2D-m, подставляем туда m=2q, получаем n/2 = 2D - 2q = 2*(D-q), <=> n = 2*2*(D-q) = 4*(D-q).
То есть n делится нацело на 4.

4,5(54 оценок)

Ответ:

Denhuk

11.12.2021

Пусть многочлен

P(x) = anxn + an–1xn–1 + ... + a0

имеет хотя бы один действительный корень и

a0 ≠ 0.

Докажите, что, последовательно вычеркивая в некотором порядке одночлены в записи P(x), можно получить из него число a0 так, чтобы каждый промежуточный многочлен также имел хотя бы один действительный корень.

Решение:

Приведем схему вычеркивания одночленов, дающую на каждом шаге многочлены, имеющие корни.

Пусть многочлен

P(x) = axn + bxm + ... + c

(a, b, c ≠ 0) содержит не менее трёх членов (xn и xm

две старших степени переменной x в P).

Если n или m нечётно, вычеркивая в P(x) одночлен bxm или axn соответственно, получим многочлен нечётной степени, имеющий хотя бы один корень.

Вычеркивая в дальнейшем другие одночлены, мы получим искомую оследовательность многочленов. Поэтому далее рассматриваем случай, когда n и m чётны.

Умножая при необходимости на –1, можем считать, что a > 0. Если c < 0, то в P(x) можно вычеркнуть любой одночлен, отличный от старшего и свободного члена, полученный многочлен P1(x) принимает отрицательное значение c при x = 0 и положительное при достаточно большом x, значит, имеет корень. Далее считаем, что c > 0.

Пусть P(t) = 0. Если b > 0, вычеркнем в P(x) одночлен bxm. При больших положительных x значение полученного многочлена P1(x) положительно, но P1(t) = P(t) – btm < 0 (так как t ≠ 0, а m чётно), следовательно P1(x) имеет корни.

Если же b < 0, вычеркнем одночлен axn, тогда значения P(x) отрицательны при больших x, но P1(0) = P(0) = c > 0, значит, он тоже имеет корни.

По приведенной схеме мы получим в конце многочлен, имеющий корни и содержащий ровно два одночлена, один из которых P(0). Утверждение доказано.

4,5(22 оценок)

Это интересно:

Стиль-и-уход-за-собой

21.06.2021

Как блокировать удар: советы от профессионалов для самозащиты...

01.10.2020

Как встречаться с парнем из другой школы: советы и техники...

Здоровье

06.07.2021

Как повысить либидо: простые способы улучшения сексуальной жизни...

Компьютеры-и-электроника

28.05.2023