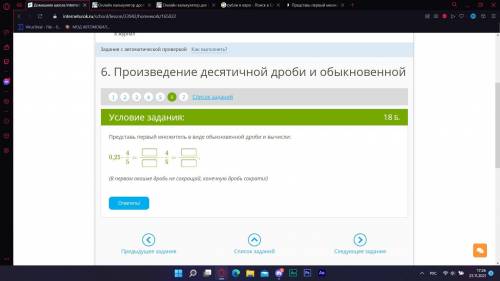
Пошаговое объяснение:
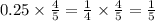
Пошаговое объяснение:
Это задача на теорему Байеса. Гипотезы:
Н1 -- взята винтовка с оптическим прицелом. Вероятность гипотезы Р (Н1) = 4/10 = 0.4.
Н2 -- взята винтовка без оптического прицела. Вероятность гипотезы Р (Н2) = 6/10 = 0.6.
Событие А -- попадание в цель. Условные вероятности попадания для каждой из гипотез: Р (А | H1) = 0.95, Р (А | H2) = 0.8.
Полная вероятность попадания: Р (А) = Р (А | H1) * Р (Н1) + Р (А | H2) * Р (Н2) = 0.4*0.95 + 0.6*0.8 = 0.86.
Апостериорная вероятность первой гипотезы при условии, что пуля попала в мишень:
P(H1 | A) = P(A | H1) * P(H1) / P(A) = 0.4*0.95/0.86.
Апостериорная вероятность второй гипотезы при условии, что пуля попала в мишень:
P(H2 | A) = P(A | H2) * P(H2) / P(A) = 0.6*0.8/0.86.
Отсюда P(H2 | A) > P(H1 | A), то есть более вероятно, что стрелок стрелял из винтовки без оптического прицела.
Для начала поймём, что вообще представляют собой заданные уравнения системы
![x^2+y^2-2bx\leq 16-b^2,\\[8pt] (x^2-2bx+b^2)+y^2\leq 4^2,\\[8pt](x-b)^2+y^2\leq 4^2](/tpl/images/2009/6197/3b998.png) - это неравенство задаёт круг радиусом
- это неравенство задаёт круг радиусом 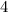 с центром в точке
с центром в точке 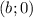 .
.
^2-5^2\leq 0,\\[8pt](x+y-7)(x+y+3)\leq 0,\\[8pt]\left[\begin{array}{@{}l@{}} \left\{\begin{array}{@{}l@{}}x+y-7\leq0\\[5pt]x+y+3\geq 0\end{array}\right.\\[18pt] \left\{\begin{array}{@{}l@{}}x+y-7\geq0\\[5pt]x+y+3\leq 0\end{array}\right. \end{array}\right.\iff\left[\begin{array}{@{}l@{}} \left\{\begin{array}{@{}l@{}}x+y\leq7\\[5pt]x+y\geq -3\end{array}\right.\\[18pt] \varnothing\end{array}\right.\iff\left\{\begin{array}{@{}l@{}}x+y\leq7\\[5pt]x+y\geq -3\end{array}\right.](/tpl/images/2009/6197/f9e72.png) - эта система задаёт полоску между прямыми
- эта система задаёт полоску между прямыми 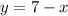 и
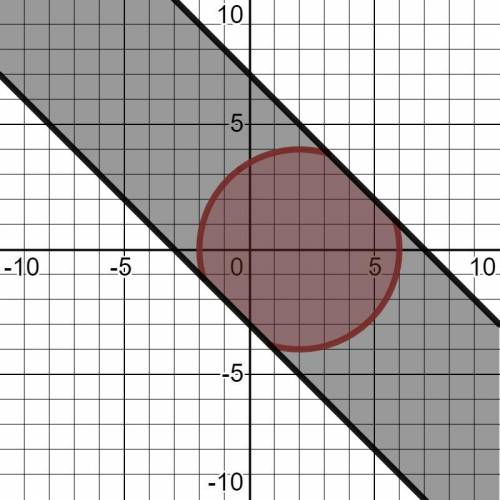
и  , включая границы (т.е. сами прямые). (См. приложенную картинку).
, включая границы (т.е. сами прямые). (См. приложенную картинку).
Таким образом, в системе оба неравенства задают пересечение указанного круга и указанной полоски.
Площадь круга радиуса 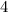 равна
равна 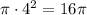 .
.
Отсюда, поскольку границы представляют собой прямые, то, при пересечении ими круга по диаметру получим нужное значение площади фигуры, т.е. половину от полной площади круга. Это можно достичь расположив центр круга в точках, где границы полоски пересекают ось 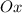 .
.
А именно при 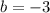 или
или 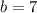 .
.
ответ. 
Пошаговое объяснение: