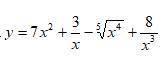
![y = 7x {}^{2} + \frac{3}{x} - \sqrt[5]{x {}^{4} } + \frac{8}{x {}^{3} }](/tpl/images/2063/3654/faf1e.png)
![y = \frac{d}{dx} (7x {}^{2} + \frac{3}{ {x}^{} } - \sqrt[5]{x {}^{4} } + \frac{8}{x {}^{3} } )](/tpl/images/2063/3654/b7fe6.png)
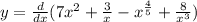
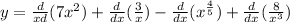
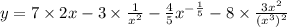
![y {}^{1} = 14x - \frac{3}{x {}^{2} } - \frac{4}{5 \sqrt[5]{x} } - \frac{24}{x {}^{4} }](/tpl/images/2063/3654/89441.png)
ответ:
ответ: х=3
решение:
log x по основанию 3 - log x по основанию 9 + log x по основанию 81 = 3/4
log x по основанию 3 - log x по основанию 3² + log x по основанию 3^4 = 3/4
log x по основанию 3 - 1/2·log x по основанию 3+ 1/4·log x по основанию 3 = 3/4
log x по основанию 3 - log (x^1/2) по основанию 3+log( x ^1/4)по основанию 3 = 3/4
log по основанию 3 от числа (( х : (x^1/2) ·( x ^1/ =3/4
log по основанию 3 от числа (х^3/4) = 3/4
3 в степени 3/4 = (х^3/4)
(х^3/4) = 3^ 3/4
х=3
ответ: х=3