Выиграть можно, если только играют двое. В игре выигрыет тот игрок, после предпоследнего хода которого остается 6 шариков, тогда после очередного хода соперника, сколько бы он не взял, в мешке останется от 1 до 5 шаров. Вытащив все их, победитель закончит игру.
Т.е. идея такова: чтобы выиграть игру надо каждый раз брать столько шаров, чтобы в сумме с шарами, взятыми перед этим партнером, они составляли 6.
Если ты хочешь выиграть и начинаешь игру, то сразу нужно взять из имеющихся 45 шаров, столько, чтобы количество оставшихся шаров было кратно 6, т.е. надо взять 3 шарика. При этом останется 42 шарика. Дальше следуем нашей идее: каждый раз надо брать столько шаров, чтобы в сумме с шарами, взятыми перед этим партнером, они составляли 6.
Если ты хочешь выиграть, но начинает соперник, нужно в последующем ходе надо взять такое количество шаров, чтобы количество оставшихся шаров стало кратно 6, т.е. в зависимости от того, сколько взял вначале соперник, берем:
соперник ты
1 2
2 1
3 Бери 3 шара, а в следующий свой ход следуй
этой же схеме, и так до тех пор, пока соперник
возьмет количество шаров не равное 3.
4 5
5 4
А дальше опять каждый раз надо брать столько шаров, чтобы в сумме с шарами, взятыми перед этим партнером, они составляли 6.
ответ: чтобы выиграть нужно начать первым, взять 3 шара, а затем брать столько шаров, чтобы в сумме с шарами, взятыми перед этим партнером, они составляли 6. Если начать вторым, есть вероятность проигрыша.
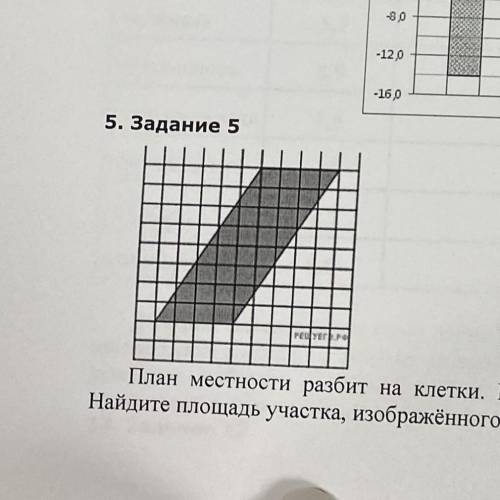
Пошаговое объяснение:
Построим до прямоугольника со сторонами
8 м и 9 м
Sпрям=8×9=72 м^2
Образовались два тр-ка с основаниями
8 м и высотой 5 м
S тр-ка=1/2×5×8=20 м^2
S участка= Sпрям-2×S тр-ка=
=72-2×20=72-40=32 м^2