1) 
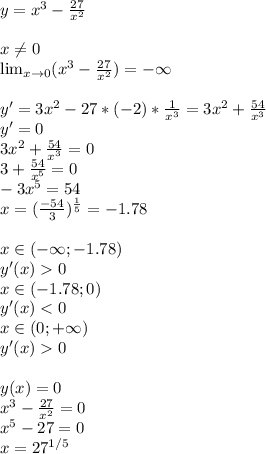
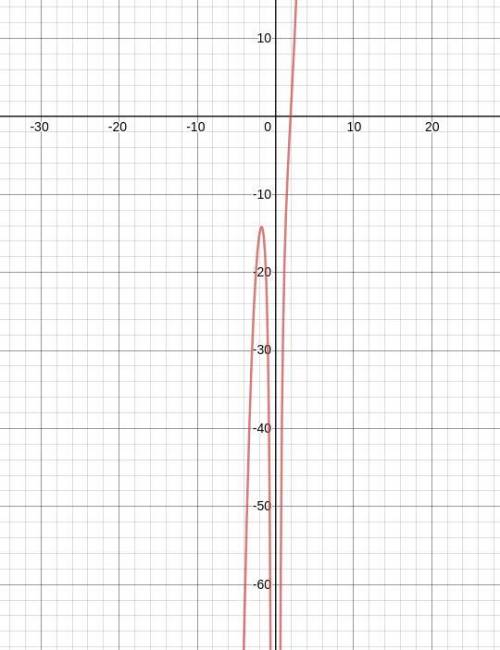
По производным понимаем где график возрастает и убывает. Также понимает что у вертикальный асимптоты x = 0 график с обеих сторон стремится к минус бесконечности. Примерно можно построить график.
Можно также уточнить род выпуклостей на частках монотонности: найти вторую производную и посмотреть ее знак на отрезках
2)
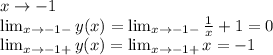
Т.к пределы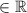 
и не равны точка 
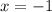является точкой конечного разрыва (первый род)
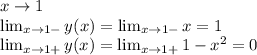
Аналогично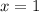 
точка конечного разрыва (первый род)
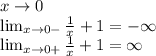
Т.к. хотя обы один предел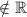 
точка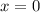 
точка рызрыва второго рода
Масса первого раствора - 2 условные единицы
Масса второго раствора - 6 условных единиц (я просто не знаю, кг, г или мг)
Пошаговое объяснение:
Пусть масса первого раствора - x
Пусть масса второго раствора - y
Тогда:
Кол-во соли в первом растворе - 0,3x
Кол-во соли во втором растворе - 0,2y
Тогда:
После смешивания получили - (0,3x + 0,2y)
Когда добавили 2 литра - 0,18(x + y + 2), где 0,18 - кол-во соли в получившемся растворе
Когда добавили 4 литра - 0,15(x + y + 4)
Тогда составим систему уравнений и решим её:
0,3x + 0,2y = 0,18(x + y + 2)
0,3x + 0,2y = 0,15(x + y + 4)
⇔
0,3x + 0,2y = 0,18x + 0,18y + 0,36
0,3x + 0,2y = 0,15x + 0,15y + 0,6
⇔
0,12x + 0,02y = 0,36
0,15x + 0,05y = 0,6
⇔
12x + 2y = 36
15x + 5y = 60
⇔
6x + y = 18
3x + y = 12
⇔
3x = 6
-y = -6
⇔
x = 2
y = 6
Пошаговое объяснение:
\ begin {gather} sin \ 2x + sin \ 6x = 0 \\ 2sin \ frac {2x + 6x} {2} cos \ frac {2x-6x} {2} = 0 \\ sin \ 4x \ cos \ 2x = 0 \\ \ left [{{sin \ 4x = O} \ atop {cos \ 2x = 0}} \ right. <=> \ left [{{4x = \ pi k} \ atop {2x = \ frac {\ pi} {2} +2 \ pi n}} \ right. <=> \ left [{{x = \ frac {\ pi k} {4} \ atop {x = \ frac {\ pi} {4} + \ pi n}} \ right. => x = \ dfrac {\ pi m} {4} \\ k \ in Z, \ n \ in Z, \ m \ in Z. \ ||| Ombem: \ \ \ dfrac {\ pi m} {4}; \ \ m \ in Z. \ end {gather}% 3D