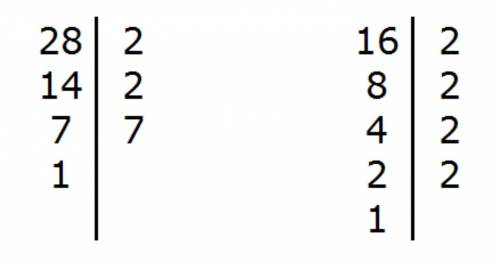
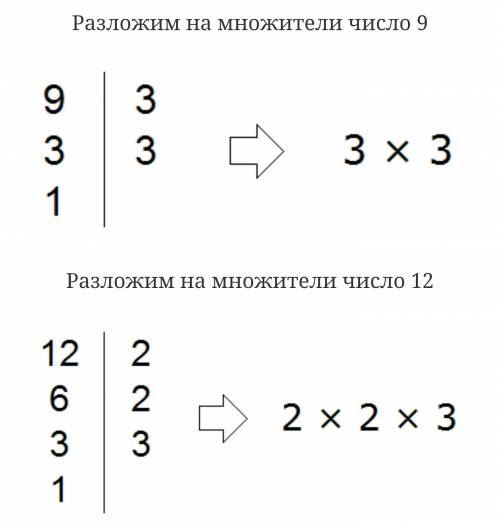
1 и 2) Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются - простыми числами. Числа, имеющие другие делители, называются составными числами.
3) Из вышесказанного следует, что единицу нельзя назвать ни простым, ни составным числом, так как простое имеет 2 делителя, а единица только один.
4) Подозреваю, что тут имеют ввиду при каких случаях получается число 24.
К примеру: 24= 2*4*3 (таких примеров довольно много).
5) Это наибольший из общих делителей.
6) Числа взаимно простые, если они не имеют никаких общих делителей, кроме ±1.
7) а) Разложить на простые множители;
б) Из этих множителей, которые входят в разложение одного из этих чисел, убрать те, которые не входятв разложении другого числа;
в) Найти произведение оставшихся чисел .
8) Наим.общ.кратное - наименьшее натуральное число, которо кратно и а и б.
9) Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
возможных равновероятных вариантов 4:
1. первый сдал и второй сдал
2. первый сдал, второй не сдал
3. первый не сдал, второй сдал
4. первый не сдал, второй не сдал
только в одном из этих вариантов ни один не сдал.
значит, вероятность, при одной попытке что хоть один сдал - 3/4 или 75%
Однако попыток две! И значит, вероятность того, что хоть один студент сдаст намного выше!
В самом деле, вариантов становиться не четыре, а 4*4 = 16 (на каждый из перечисленных вариантов первой попытки приходится по четыре варианта второй попытки), при чем только один из этих 16 вариантов - когда ни один студент не сдал. То есть вероятность сдачи лабораторной работы хотя бы одним студентом при двух попытках становится 15/16
Все бы хорошо, но можно задаться вопросом - следует ли учитывать все 16 вариантов: ведь второй попытки студенту, сдавшему работу при первой попытке, не будет дано. Тогда расклады такие:
1. оба сдали
2.1. первый сдал, второй не сдал, при второй попытке второй не сдал
2.2. первый сдал, второй не сдал, при второй попытке второй сдал
3.1. первый не сдал, второй сдал, при второй попытке первый не сдал
3.2. первый не сдал, второй сдал, при второй попытке первый сдал
4.1. оба не сдали, при второй попытке оба сдали
4.2. оба не сдали, при второй попытке первый сдал, второй не сдал
4.3. оба не сдали, при второй попытке первый не сдал, второй сдал
4.4. оба не сдали, при второй попытке оба снова не сдали
как видно, при таком подсчета получилось всего 9 вариантов, и только один из них, в котором оба не сдали. То есть здесь вероятность того, что хотя бы один сдаст равна 8/9
теперь я и сам запутался - который из вариантов нужно считать верным ответом)))
P.S. Тока вот дрянненький у них препод, если сдача лабораторной - вопрос вероятности, а не результат знаний студентов... будто они монетку бросают))