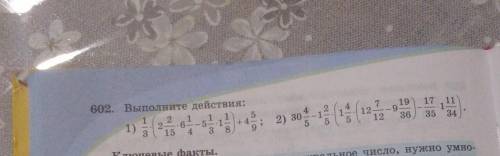
1) (1/3)*((32/15)*(25/4)-(16/3)*(9/8))+4 5/9=1/3*((8*5/3)-(2*9/3))+4 5/9=
(40-18)/9+ 4 5/9=22/9+4 5/9=2 4/9+4 5/9=7
2) выполним по действиям
1) 12 7/12-9 19/36= 12 21/36 -9 19/36= 3 2/36= 3 1/18=55/18;
2) 1 4/5* (55/18)=(9/5)*(55/18)=11/2= 5 1/2;
3) 17/35*(1 11/34)=(17/35)* (45/34)=(17*45)/(35*34)=9/(7*2)=9/14;
4)5 1/2- 9/14=4 3/2-9/14=4(21-9)/14=4 12/14=4 6/7=34/7
5)1 2/5 *(34/7)=(7/5)*(34/7)=34/5=6 4/5
6) 30 4/5 -6 4/5=24
Произведение обратных чисел равно единице.
2 4/5 + 1,2 = 2 4/5 + 1 1/5 = 3 5/5 = 4 - сумма чисел
Обратное число 1/4.
Проверка: 4 · 1/4 = 1.
- - - - - - - - - - - - - - - - - - - -
2 4/5 - 1,2 = 2 4/5 - 1 1/5 = 1 3/5 = 8/5 - разность чисел
Обратное число 5/8.
Проверка: 8/5 · 5/8 = 1.
- - - - - - - - - - - - - - - - - - - -
2 4/5 · 1,2 = 14/5 · 6/5 = 84/25 - произведение чисел
Обратное число 25/84.
Проверка: 84/25 · 25/84 = 1.
- - - - - - - - - - - - - - - - - - - -
2 4/5 : 1,2 = 14/5 : 6/5 = 14/5 · 5/6 = 7/3 - частное чисел
Обратное число 3/7.
Проверка: 7/3 · 3/7 = 1.
Пошаговое объяснение:
5cos²x - 6cosx + 1 = 0,
cosx = а,
5а² - 6а + 1 = 0,
Д = (-6)² - 4*5*1 = 36 - 20 = 16,
а1 = (6 + 4) / 2*5 = 10/10 = 1,
а2 = (6 - 4) / 2*5 = 2/10 = 1/5,
cosx = а1,
cosx = 1,
х1 = 2πn, n ∈ Z,
cosx = а2,
cosx = 1/5,
х2 = ±arccos (1/5) + 2πn, n ∈ Z,
2ctgx - 3tgx + 1 = 0,
2/(tgx) - 3tgx + 1 = 0, (* tgx)
2tgx - 3tg²x + 1 = 0,
3tg²x - 2tgx - 1 = 0,
tgx = а,
3а² - 2а - 1 = 0,
Д = (-2)² - 4*3*(-1) = 4 + 12 = 16,
а1 = (2 + 4) / 2*3 = 6/6 = 1,
а2 = (2 - 4) / 2*3 = -2/6 = -1/3,
tgx = а1,
tgx = 1,
х = arctg1 + πn, n ∈ Z,
x = π/4 + πn, n ∈ Z,
tgx = а2,
tgx = -1/3,
∅
Пошаговое объяснение:
1. 1/3×(32/15×25/4×16/3×9/8)=1/3×240/3=1/3×=80/3;
80/3+41/9=281/9=31 2/9
2. 151/12-343/36=453/36-343/36=110/36=55/18=3 1/18
55/18×9/5=11/2=5 1/2
17/35×45/34=9/14
11/2-9/14=77/14-9/14=68/14=4 12/14=4 6/7;
34/7×7/5=34/5;
154/5-34/5=120/5=24